FAQ

Team Algoritma

March 16, 2021

Pendahuluan

Algoritma menyediakan pelatihan untuk membantu para pekerja profesional maupun pelajar untuk mencapai keterampilan dasar dalam berbagi bidang data science yang terdiri dari: Data Visualization, Machine Learning, Data Modelling, Inferensial Statistik, dll. Kumpulan FAQ ini diproduksi oleh tim Algoritma untuk membantu para peserta Data Science Academy atau khalayak umum mengenai pertanyaan pertanyaan yang sering ditemukan mengenai topik machine learning.

Bab 1 Data Wrangling

1.1 Regular Expression

1.1.1 Bagaimana cara membuat nama kolom menjadi lebih rapih saat dilakukan visualisasi?

names(vids)

#>  [1] "trending_date"          "title"                  "channel_title"         
#>  [4] "category_id"            "publish_time"           "views"                 
#>  [7] "likes"                  "dislikes"               "comment_count"         
#> [10] "comments_disabled"      "ratings_disabled"       "video_error_or_removed"

Untuk membuat tampilan visualisasi menjadi lebih rapih kita dapat mengubah nama kolom menggunakan function str_replace() dan str_to_title(). Function str_replace() akan mengubah nama kolom dengan menghapus pattern "_". Sedangkan function str_to_title() akan membuat huruf awal setiap kata menjadi uppercase.

names(vids) %>% 
  str_replace(pattern = "_",
              replacement = " ") %>% 
  str_to_title()

#>  [1] "Trending Date"          "Title"                  "Channel Title"         
#>  [4] "Category Id"            "Publish Time"           "Views"                 
#>  [7] "Likes"                  "Dislikes"               "Comment Count"         
#> [10] "Comments Disabled"      "Ratings Disabled"       "Video Error_or_removed"

1.1.2 Bagaimana cara mengubah nama kolom dengan bentuk (pattern) tertentu?

Pada data laporan kita memiliki kolom “hasil_pajak_daerah”, “hasil_retribusi_daerah”, “hasil_pengelolaan_kekayaan_daerah_yang_dipisahkan”. Berikut ini kita akan mengubah nama kolom yang memiliki pattern hasil_ diubah menjadi total_ menggunakan function str_replace()

paged_table(laporan)

ABCDEFGHIJ0123456789

daerah <chr>	provinsi <chr>	jenis <chr>
Kab Aceh Barat	Aceh	Anggaran
Kab Aceh Besar	Aceh	Anggaran
Kab Aceh Selatan	Aceh	Anggaran
Kab Aceh Singkil	Aceh	Anggaran
Kab Aceh Tengah	Aceh	Anggaran
Kab Aceh Tenggara	Aceh	Anggaran
Kab Aceh Timur	Aceh	Anggaran
Kab Aceh Utara	Aceh	Anggaran
Kab Bireun	Aceh	Anggaran
Kab Pidie	Aceh	Anggaran

Next

123456

...

508

Previous

1-10 of 5,080 rows | 1-3 of 25 columns

names(laporan) %>% 
  str_replace(pattern = "hasil_",
              replacement =  "total_")

#>  [1] "daerah"                                                           
#>  [2] "provinsi"                                                         
#>  [3] "jenis"                                                            
#>  [4] "periode"                                                          
#>  [5] "pendapatan_daerah"                                                
#>  [6] "pendapatan_asli_daerah"                                           
#>  [7] "total_pajak_daerah"                                               
#>  [8] "total_retribusi_daerah"                                           
#>  [9] "total_pengelolaan_kekayaan_daerah_yang_dipisahkan"                
#> [10] "lain_lain_pendapatan_asli_daerah_yang_sah"                        
#> [11] "dana_perimbangan"                                                 
#> [12] "dana_bagi_total_pajak_bagi_hasil_bukan_pajak"                     
#> [13] "dana_alokasi_umum"                                                
#> [14] "dana_alokasi_khusus"                                              
#> [15] "lain_lain_pendapatan_daerah_yang_sah"                             
#> [16] "pendapatan_hibah"                                                 
#> [17] "dana_darurat"                                                     
#> [18] "dana_bagi_total_pajak_dari_provinsi_dan_pemerintah_daerah_lainnya"
#> [19] "dana_penyesuaian_dan_otonomi_khusus"                              
#> [20] "bantuan_keuangan_dari_provinsi_atau_pemerintah_daerah_lainnya"    
#> [21] "pendapatan_lain_lain"                                             
#> [22] "belanja_daerah"                                                   
#> [23] "belanja_pegawai_l"                                                
#> [24] "belanja_barang_dan_jasa"                                          
#> [25] "belanja_modal"

1.1.3 Bagaimana cara menggabungkan dua atau lebih vector ke dalam satu vector?

Kita dapat menggunakan function str_c() sebagai berikut:

str_c(c("Music","Gaming","Shows"), collapse = ",")

#> [1] "Music,Gaming,Shows"

Function str_c() juga dapat digunakan untuk membuat vector dengan pattern yang berulang sebagai berikut:

str_c("Laporan", c(2017:2020),"Q1",sep = "-")

#> [1] "Laporan-2017-Q1" "Laporan-2018-Q1" "Laporan-2019-Q1" "Laporan-2020-Q1"

1.1.4 Apa perbedaan dari function str_replace() dan str_replace_all()?

dat <- c("data","science","algoritma")

Ketika menggunakan function str_replace() akan mengubah pattern pertama yang ditemui, sebagai berikut:

str_replace(dat,"[aiueo]","-")

#> [1] "d-ta"      "sc-ence"   "-lgoritma"

Sedangkan function str_replace_all() akan mengubah semua pattern yang ditemui pada vector, sebagai berikut:

str_replace_all(dat,"[aiueo]","-")

#> [1] "d-t-"      "sc--nc-"   "-lg-r-tm-"

1.2 Working Datetime

1.2.1 Bagaimana cara mengubah variabel/kolom bertipe “character” menjadi “date”, jika dalam 1 kolom terdapat format (urutan) tanggal yang berbeda?

Untuk mengubah tipe data “character” menjadi “date” pada kolom yang memiliki format (urutan) tanggal yang berbeda-beda, dapat mnggunakan fungsi parse_date() dari library parsedate.

# membuat sebuah vector yang berisi tanggal dengan format yang berbeda
tanggal <- c("1-January-2020", "01/01/20", "12-31-2019")

tanggal <- parsedate::parse_date(tanggal)

class(tanggal)

#> [1] "POSIXct" "POSIXt"

tanggal

#> [1] "2020-01-01 UTC" "2020-01-01 UTC" "2019-12-31 UTC"

1.3 Data Transformation with dplyr

1.3.1 Bagaimana cara melakukan subsetting baris (filter) terhadap baris-baris yang sama dengan beberapa nilai? Misal, akan dilakukan filter terhadap baris-baris yang memiliki ketegori (category_id) Comedy, Music, atau Gaming?

Untuk melakukan filter terhadap baris-baris yang sama dengan beberapa nilai (lebih dari satu nilai), dapat menggunakan operator atau | ataupun menggunakan operator inlude %in%.

unique(vids$category_id)

#>  [1] People and Blogs       Entertainment          Comedy                
#>  [4] Science and Technology Film and Animation     News and Politics     
#>  [7] Sports                 Music                  Pets and Animals      
#> [10] Education              Howto and Style        Autos and Vehicles    
#> [13] Travel and Events      Gaming                 Nonprofit and Activism
#> [16] Shows                 
#> 16 Levels: Autos and Vehicles Comedy Education ... Travel and Events

filter1 <- vids %>% 
  filter(category_id == "Comedy" | category_id == "Music" | category_id == "Gaming")
  
unique(filter1$category_id)

#> [1] Comedy Music  Gaming
#> 16 Levels: Autos and Vehicles Comedy Education ... Travel and Events

# code di atas dapat disederhanakan menjadi
filter1 <- vids %>% 
  filter(category_id %in% c("Gaming", "Music", "Comedy"))

unique(filter1$category_id)

#> [1] Comedy Music  Gaming
#> 16 Levels: Autos and Vehicles Comedy Education ... Travel and Events

Berikut contoh kasus jika baris-baris yang ingin dipilih tidak sama dengan beberapa nilai (lebih dari satu nilai), dapat menggunakan operator dan & ataupun menggunakan operator include %in% yang digabungkan dengan operator tidak !.

filter2 <- vids %>% 
  filter(category_id != "Comedy" & category_id != "Music" & category_id != "Gaming")
  
unique(filter2$category_id)

#>  [1] People and Blogs       Entertainment          Science and Technology
#>  [4] Film and Animation     News and Politics      Sports                
#>  [7] Pets and Animals       Education              Howto and Style       
#> [10] Autos and Vehicles     Travel and Events      Nonprofit and Activism
#> [13] Shows                 
#> 16 Levels: Autos and Vehicles Comedy Education ... Travel and Events

# code di atas dapat disederhanakan menjadi
filter2 <- vids %>% 
  filter(!category_id %in% c("Comedy", "Music", "Gaming"))
  
unique(filter2$category_id)

#>  [1] People and Blogs       Entertainment          Science and Technology
#>  [4] Film and Animation     News and Politics      Sports                
#>  [7] Pets and Animals       Education              Howto and Style       
#> [10] Autos and Vehicles     Travel and Events      Nonprofit and Activism
#> [13] Shows                 
#> 16 Levels: Autos and Vehicles Comedy Education ... Travel and Events

1.3.2 Bagaimana cara menampilkan kolom yang memiliki unsur kata dana?

Untuk menampilkan kolom dengan kata (term) tertentu dapat menggunakan function select_at() dari package dplyr:

laporan %>% 
  select_at(.vars = vars(contains("dana"))) %>% 
  head()

#>   dana_perimbangan dana_bagi_hasil_pajak_bagi_hasil_bukan_pajak
#> 1     782044000000                                  21953000000
#> 2     977082000000                                  22236000000
#> 3     983548000000                                  17732000000
#> 4     598216000000                                  18482000000
#> 5     841794000000                                  16607000000
#> 6     799735000000                                  14301000000
#>   dana_alokasi_umum dana_alokasi_khusus dana_darurat
#> 1      570764000000        189327000000            0
#> 2      713345000000        241502000000            0
#> 3      641605000000        324211000000            0
#> 4      441266000000        138468000000            0
#> 5      603737000000        221449000000            0
#> 6      586091000000        199342000000            0
#>   dana_bagi_hasil_pajak_dari_provinsi_dan_pemerintah_daerah_lainnya
#> 1                                                       24441000000
#> 2                                                       29527000000
#> 3                                                       30141000000
#> 4                                                       20609000000
#> 5                                                       29389000000
#> 6                                                       42186000000
#>   dana_penyesuaian_dan_otonomi_khusus
#> 1                        256083000000
#> 2                        412171000000
#> 3                        216237000000
#> 4                         90964000000
#> 5                        232677000000
#> 6                        252239000000

1.3.3 Bagaimana cara menampilkan kolom dengan lebih dari satu kata (term) tertentu?

Berikut ini kita akan menampilkan kolom yang memiliki unsur Pendapatan atau Daerah dengan bantuan function matches() dari package dplyr

laporan %>% 
  select_at(.vars = vars(matches("Pendapatan|Daerah"))) %>% 
  head()

#>              daerah pendapatan_daerah pendapatan_asli_daerah hasil_pajak_daerah
#> 1    Kab Aceh Barat     1251178000000           164141000000        16170000000
#> 2    Kab Aceh Besar     1662846000000           132396000000        60500000000
#> 3  Kab Aceh Selatan     1396406000000           165862000000        10570000000
#> 4  Kab Aceh Singkil      785724000000            55233000000        10645000000
#> 5   Kab Aceh Tengah     1286924000000           183064000000        11374000000
#> 6 Kab Aceh Tenggara     1168068000000            73908000000        11715000000
#>   hasil_retribusi_daerah hasil_pengelolaan_kekayaan_daerah_yang_dipisahkan
#> 1             9410000000                                        4916000000
#> 2             5910000000                                        3500000000
#> 3             9346000000                                        5200000000
#> 4            25836000000                                        3378000000
#> 5            12565000000                                        5300000000
#> 6             2115000000                                        3000000000
#>   lain_lain_pendapatan_asli_daerah_yang_sah
#> 1                              133644000000
#> 2                               62487000000
#> 3                              140746000000
#> 4                               15374000000
#> 5                              153826000000
#> 6                               57078000000
#>   lain_lain_pendapatan_daerah_yang_sah pendapatan_hibah
#> 1                         304994000000      24470000000
#> 2                         553368000000      31670000000
#> 3                         246995000000        618000000
#> 4                         132275000000      20702000000
#> 5                         262065000000                0
#> 6                         294425000000                0
#>   dana_bagi_hasil_pajak_dari_provinsi_dan_pemerintah_daerah_lainnya
#> 1                                                       24441000000
#> 2                                                       29527000000
#> 3                                                       30141000000
#> 4                                                       20609000000
#> 5                                                       29389000000
#> 6                                                       42186000000
#>   bantuan_keuangan_dari_provinsi_atau_pemerintah_daerah_lainnya
#> 1                                                             0
#> 2                                                   80000000000
#> 3                                                             0
#> 4                                                             0
#> 5                                                             0
#> 6                                                             0
#>   pendapatan_lain_lain belanja_daerah
#> 1                    0  1278780000000
#> 2                    0  1757856000000
#> 3                    0  1410406000000
#> 4                    0   794579000000
#> 5                    0  1287177000000
#> 6                    0  1257654000000

1.3.4 Bagaimana cara menampilkan kolom dengan kata (term) awalan atau akhiran tertentu?

Untuk meampilkan kolom yang diawali dengan kata Dana atau diakhiri dengan kata pajak dapat menggunakan bantuan function starts_with() dan ends_with() dari package dplyr

laporan %>% 
  select(starts_with("Dana")) %>% 
  head()

#>   dana_perimbangan dana_bagi_hasil_pajak_bagi_hasil_bukan_pajak
#> 1     782044000000                                  21953000000
#> 2     977082000000                                  22236000000
#> 3     983548000000                                  17732000000
#> 4     598216000000                                  18482000000
#> 5     841794000000                                  16607000000
#> 6     799735000000                                  14301000000
#>   dana_alokasi_umum dana_alokasi_khusus dana_darurat
#> 1      570764000000        189327000000            0
#> 2      713345000000        241502000000            0
#> 3      641605000000        324211000000            0
#> 4      441266000000        138468000000            0
#> 5      603737000000        221449000000            0
#> 6      586091000000        199342000000            0
#>   dana_bagi_hasil_pajak_dari_provinsi_dan_pemerintah_daerah_lainnya
#> 1                                                       24441000000
#> 2                                                       29527000000
#> 3                                                       30141000000
#> 4                                                       20609000000
#> 5                                                       29389000000
#> 6                                                       42186000000
#>   dana_penyesuaian_dan_otonomi_khusus
#> 1                        256083000000
#> 2                        412171000000
#> 3                        216237000000
#> 4                         90964000000
#> 5                        232677000000
#> 6                        252239000000

laporan %>% 
  select(ends_with("pajak")) %>% 
  head()

#>   dana_bagi_hasil_pajak_bagi_hasil_bukan_pajak
#> 1                                  21953000000
#> 2                                  22236000000
#> 3                                  17732000000
#> 4                                  18482000000
#> 5                                  16607000000
#> 6                                  14301000000

1.3.5 Bagaimana cara menampilkan data teratas untuk setiap kategori dari variabel tertentu?

Berikut ini kita akan menampilkan jenis Anggaran terbaru untuk setiap provinsi, langkah yang dilakukan sebagai berikut:

- Melakukan filter pada kolom jenis untuk tipe "Anggaran"
- Mengurutkan periode dari yang terbaru hingga terlama
- Melakukan grouping berdasarkan `provinsi`
- Menampilkan 1 data teratas untuk setiap provinsi

Output berikut ini menampilkan Anggaran terbaru dari setiap provinsi:

laporan %>% 
  filter(
    jenis == "Anggaran"
  ) %>% 
  arrange(daerah, desc(periode)) %>% 
  group_by(provinsi) %>% 
  slice(1)

#> # A tibble: 34 x 25
#> # Groups:   provinsi [34]
#>    daerah provinsi jenis periode pendapatan_daer~ pendapatan_asli~
#>    <chr>  <chr>    <chr> <chr>              <dbl>            <dbl>
#>  1 Kab A~ Aceh     Angg~ 2018-0~    1251178000000     164141000000
#>  2 Kab B~ Bali     Angg~ 2018-0~    6567484000000    5700511000000
#>  3 Kab B~ Bangka ~ Angg~ 2018-0~    1045407000000     140835000000
#>  4 Kab L~ Banten   Angg~ 2018-0~    2414034000000     299733000000
#>  5 Kab B~ Bengkulu Angg~ 2018-0~     900262000000      58720000000
#>  6 Kab B~ DI Yogy~ Angg~ 2018-0~    2056183000000     420143000000
#>  7 Prov ~ DKI Jak~ Angg~ 2018-0~   66029983000000   44570508000000
#>  8 Kab B~ Goronta~ Angg~ 2018-0~     828164000000      46238000000
#>  9 Kab B~ Jambi    Angg~ 2018-0~    1246198000000     112000000000
#> 10 Kab B~ Jawa Ba~ Angg~ 2018-0~    5064214000000     813568000000
#> # ... with 24 more rows, and 19 more variables: hasil_pajak_daerah <dbl>,
#> #   hasil_retribusi_daerah <dbl>,
#> #   hasil_pengelolaan_kekayaan_daerah_yang_dipisahkan <dbl>,
#> #   lain_lain_pendapatan_asli_daerah_yang_sah <dbl>, dana_perimbangan <dbl>,
#> #   dana_bagi_hasil_pajak_bagi_hasil_bukan_pajak <dbl>,
#> #   dana_alokasi_umum <dbl>, dana_alokasi_khusus <dbl>,
#> #   lain_lain_pendapatan_daerah_yang_sah <dbl>, pendapatan_hibah <dbl>,
#> #   dana_darurat <dbl>,
#> #   dana_bagi_hasil_pajak_dari_provinsi_dan_pemerintah_daerah_lainnya <dbl>,
#> #   dana_penyesuaian_dan_otonomi_khusus <dbl>,
#> #   bantuan_keuangan_dari_provinsi_atau_pemerintah_daerah_lainnya <dbl>,
#> #   pendapatan_lain_lain <dbl>, belanja_daerah <dbl>, belanja_pegawai_l <dbl>,
#> #   belanja_barang_dan_jasa <dbl>, belanja_modal <dbl>

1.3.6 Bagaimana cara untuk memisahkan beberapa nilai pada 1 baris/observasi di kolom tertentu ke dalam beberapa kolom?

Berikut ini kita memiliki variabel product yang berisikan berbagai macam product yang dibeli oleh customer, bagaimana cara kita untuk memisahkan variabel tersebut menjadi beberapa kolom untuk setiap product yang dibeli?

#>   id            product
#> 1  1       Milk, Cereal
#> 2  2 Coffe, Sugar, Milk
#> 3  3              Bread
#> 4  4  Tea, Sugar, Bread

Kita dapat menggunakan function separate() dari package tidyr sebagai berikut:

dat %>% 
  separate(col = "product",
           into = str_c("Product",1:3, sep = "-"),
           sep = ", ")

#>   id Product-1 Product-2 Product-3
#> 1  1      Milk    Cereal      <NA>
#> 2  2     Coffe     Sugar      Milk
#> 3  3     Bread      <NA>      <NA>
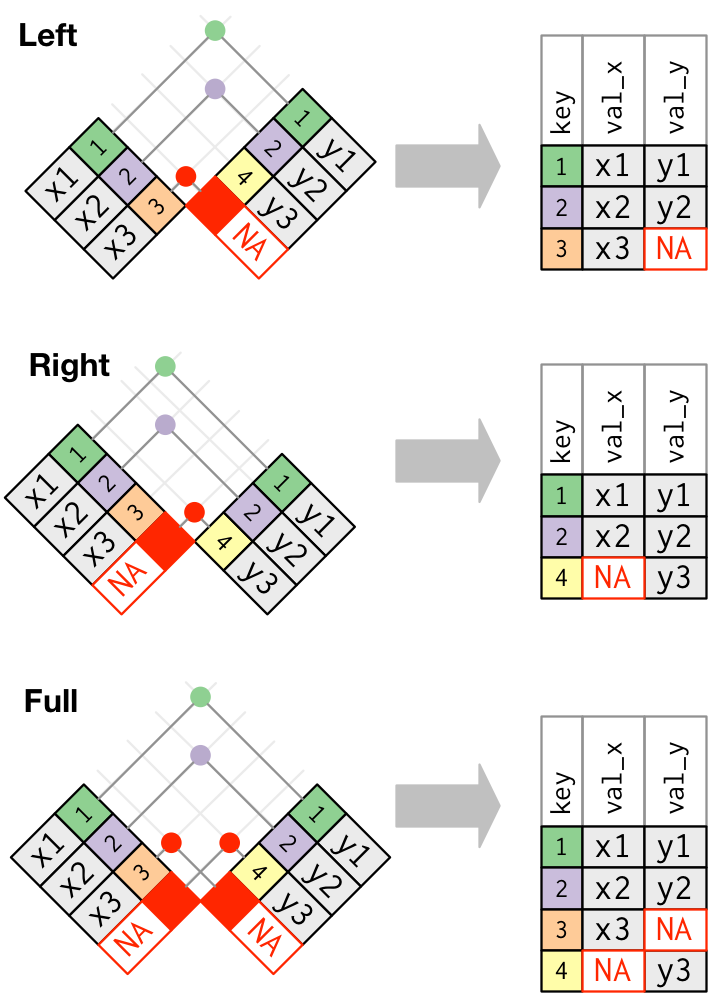
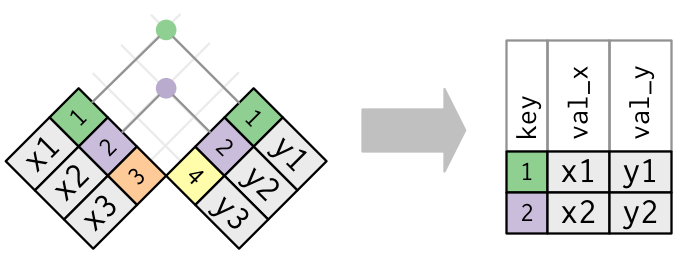
#> 4  4       Tea     Sugar     Bread

1.3.7 Apa perbedaan dari left_join, right_join, full_join, dan inner_join?

• Function left_join() akan mempertahankan observasi X
• Function right_join() akan mempertahankan observasi Y
• Function full_join() akan menampilkan observasi yang berada pada data X atau Y
• Function inner_join() akan menampilkan observasi yang terdapat pada data X dan Y.

Source: R For Data Science

Inner join

1.3.8 Bagaimana cara menghilangkan bahasa latin pada data?

Untuk menghilangkan bahasa latin pada data dapat menggunakan fungsi stri_trans_general() dari library stringi

dat <- "Special,  satisfação, Happy, Sad, Potential, für"
dat

#> [1] "Special,  satisfação, Happy, Sad, Potential, für"

library(stringi)
stri_trans_general(dat, "latin-ascii")

#> [1] "Special,  satisfacao, Happy, Sad, Potential, fur"

1.4 Handling Missing Value

1.4.1 Bagaimana cara mengatasi missing value pada data?

Salah satu cara menangani missing value adalah melakukan imputation atau mengisi missing value dengan suatu nilai. Package tidyr menyediakan function fill() yang berfungsi untuk mengisi missing value menggunakan nilai observasi berikutnya atau sebelumnya.

#> # A tibble: 4 x 3
#>   person           treatment response
#>   <chr>                <dbl>    <dbl>
#> 1 Derrick Whitmore         1        7
#> 2 <NA>                     2       10
#> 3 <NA>                     3        9
#> 4 Katherine Burke          1        4

Function fill() memiliki parameter direction untuk mengatur arah nilai yang akan diisi. Parameter direction terdiri dari “down”, “up”, “downup”, dan “updown”.

treatment %>% 
  fill(person,.direction = "down")

#> # A tibble: 4 x 3
#>   person           treatment response
#>   <chr>                <dbl>    <dbl>
#> 1 Derrick Whitmore         1        7
#> 2 Derrick Whitmore         2       10
#> 3 Derrick Whitmore         3        9
#> 4 Katherine Burke          1        4

Tentunya penanganan tersebut tidak dapat diterapkan untuk semua data, penanganan ini dapat digunakan untuk format data yang memiliki nilai tidak berulang.

1.5 DB Connections

Bagaimana mengkoneksikan database ke R?

1.5.1 MySQL

Connecting to MySQL from R

# 1. Library
library(RMySQL)

# 2. Settings
db_user <- 'mydatabase_admin'
db_password <- 'bintang123#'
db_name <- 'iris'
db_table <- 'irisData'
db_host <- '127.0.0.1' # for local access
db_port <- 3306

mydb <-  dbConnect(MySQL(), 
                   user = db_user, 
                   password = db_password,
                   dbname = db_name, 
                   host = db_host, 
                   port = db_port)

# 3. Read data from db
# SELECT * FROM irisData LIMIT 5
s <- paste0("select * from ", db_table, " limit 5")
rs <- dbSendQuery(mydb, s)
df <-  fetch(rs)
on.exit(dbDisconnect(mydb))

1.5.2 SQL Server

Connecting to SQL Server from R

# 1. Library
library(DBI)
library(odbc)

# list driver
sort(unique(odbcListDrivers()[[1]]))

# 2. Settings
conn <- dbConnect(odbc(),
                  Driver = "SQL Server", # check your odbcinst.ini
                  Server = "localhost\\SQLEXPRESS", # server ip address
                  Port = 3306, 
                  UID = "mydatabase_admin", # username
                  PWD = "bintang123#", # password
                  Database = "iris") # database name

1.5.3 SQLite

Connecting to SQLite from R

1. database

# 1. Library
library(RSQLite)
library(DBI)

# 2. Settings
conn <- dbConnect(SQLite(), 
                  host = '127.0.0.1', # for local host 
                  port = 3306,
                  user = 'mydatabase_admin',
                  password = 'bintang123#',
                  db = 'iris')

2. local file

# 1. Library
library(RSQLite)
library(DBI)

# 2. Settings
connection <- dbConnect(SQLite(), "data_input/flights.db")

# 3. Read data from db (local file)
dbListTables(connection)

s <- "select * from airports limit 5"
rs <- dbSendQuery(connection, s)
df <-  fetch(rs, n = -1)

1.5.4 Oracle

• Connecting to Oracle from R
• R to Oracle Database Connectivity
• How to Connect to Database in R

# 1. Library
library(DBI)
library(odbc)
library(RODBC)

# 2. Settings
con <- dbConnect(odbc(),
                 Driver = "[your driver's name]",
                 Host   = "[your server's path]",
                 SVC    = "[your schema's name]",
                 UID    = "Database user",
                 PWD    = "Database password",
                 Port   = 1521)

# 1. Library
library(DBI)
library(odbc)
library(RJDBC)

# 2. Settings
drv <- JDBC("oracle.jdbc.OracleDriver",
classPath="…tklocal/instantclient_11_2/ojdbc5.jar"," ")
con <- dbConnect(Driver = drv, 
                 Host = " jdbc:oracle:thin:@myHost:1521:db", 
                 UID = "user",
                 PWD = "pass")

Bab 2 Data Visualization & Interactive Plotting

2.1 Data Visualization

2.1.1 Base Plot

2.1.2 Geom

2.1.2.1 Bagaimana cara menambahkan separator (,) untuk memisahkan angka ribuan pada label geom_text()/geom_label() yang terletak pada setiap batang (bar) di bar plot?

Untuk menambahkan separator (,) dengan tujuan memisahkan angka ribuan pada label geom_text()/geom_label() yang terletak pada setiap batang di bar plot, bisa menggunakan fungsi comma() dari package scales.

vids1 <- vids %>% 
  filter(category_id %in% c("Education", "Science and Technology")) %>% 
  group_by(channel_title, category_id) %>% 
  summarise(total.likes = sum(likes)) %>% 
  ungroup() %>% 
  arrange(desc(total.likes)) %>% 
  head(5)

ggplot(vids1, aes(x = total.likes,y = reorder(channel_title, total.likes))) +
  geom_col(aes(fill = total.likes), show.legend = F) +
  labs(title = "Top 5 Channel based on Total Likes",
       subtitle = "Category: Education & Science and Technology",
       x = "Channel",
       y = NULL,
       caption = "Source: Algoritma") +
  geom_label(aes(label = comma(total.likes)), hjust = 1.05) +
  scale_fill_gradient(low = "red", high = "black") +
  theme_minimal()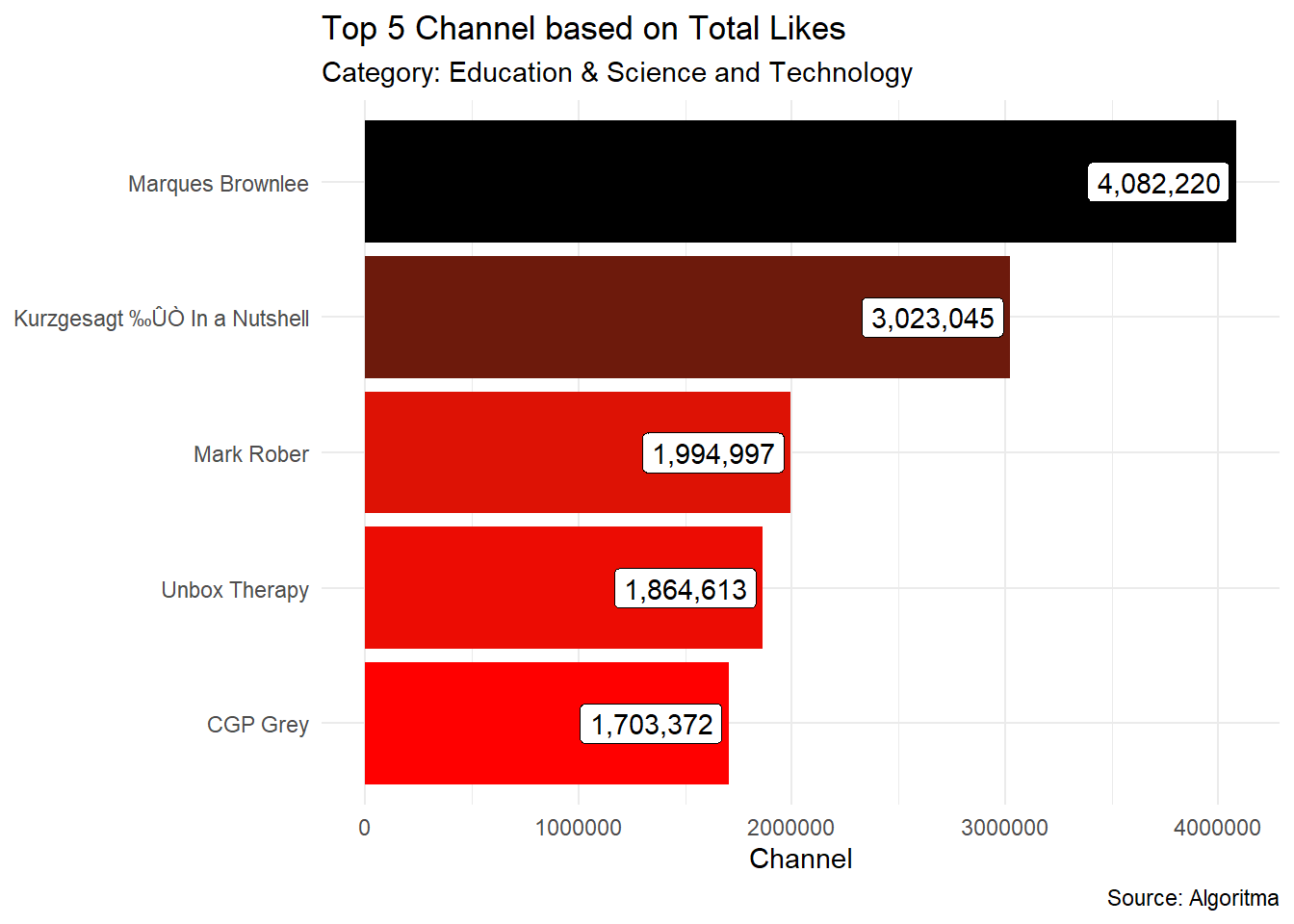

2.1.2.2 Bagaimana cara untuk mengurutkan batang (bar) saat menggunakan geom_bar()?

Untuk mengurutkan batang ketika menggunakan geom_bar kita dapat menggunakan function fct_infreq() dari package forcats, kemudian untuk mengatur bar dari paling besar hingga paling kecil kita dapat menggunakan bantuan function fct_rev().

ggplot(data = vids.u, mapping = aes(y = fct_rev(fct_infreq(category_id))))+
  geom_bar() +
  labs( x = "Category",
        y = "Total Video")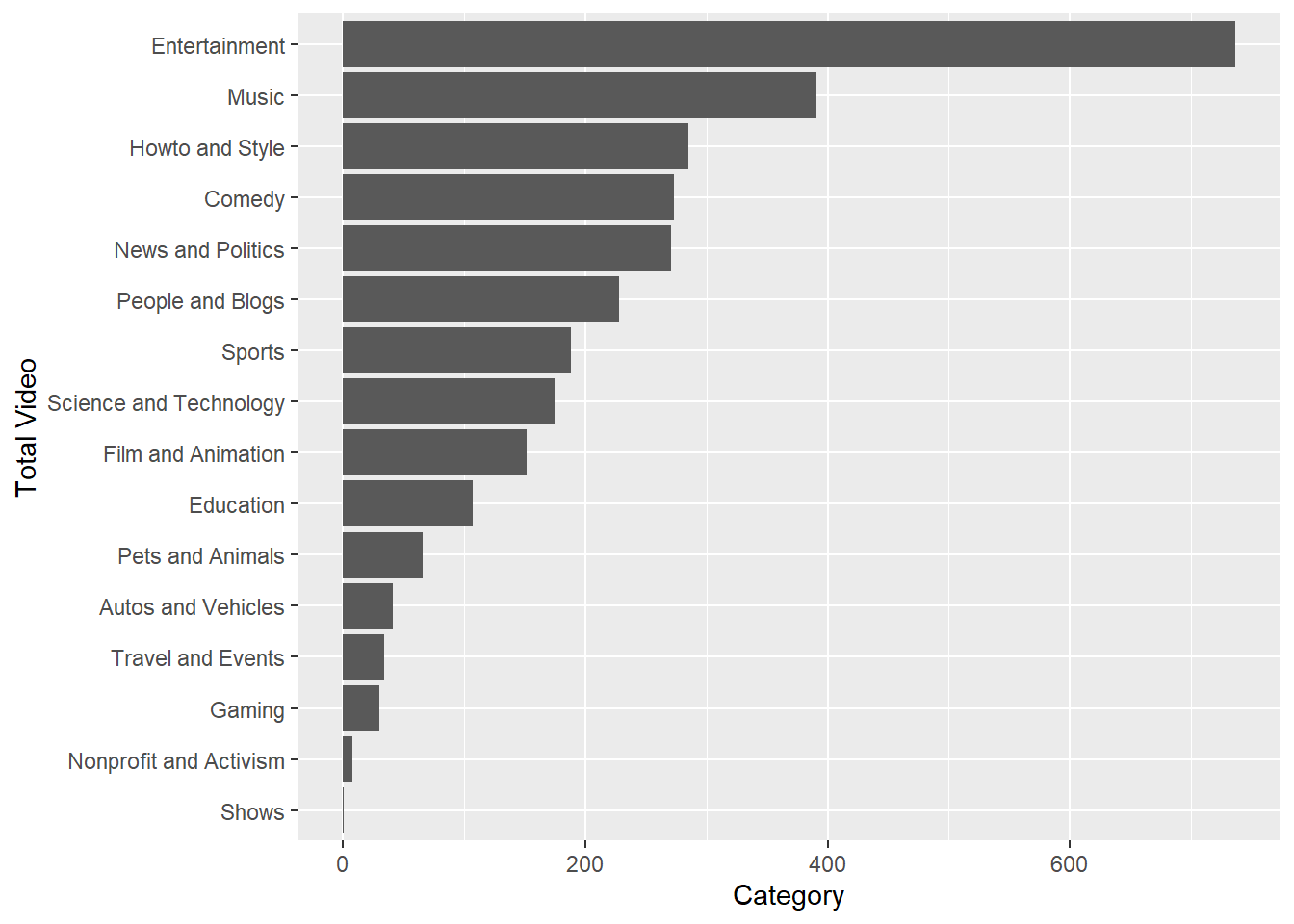

2.1.2.3 Bagaimana cara mengubah urutan kategori pada legend?

ggplot(data = iris, aes(x = Species,y = Sepal.Length))+
  geom_boxplot(aes(color = Species))+
  scale_color_manual(values = c("red","blue","green"))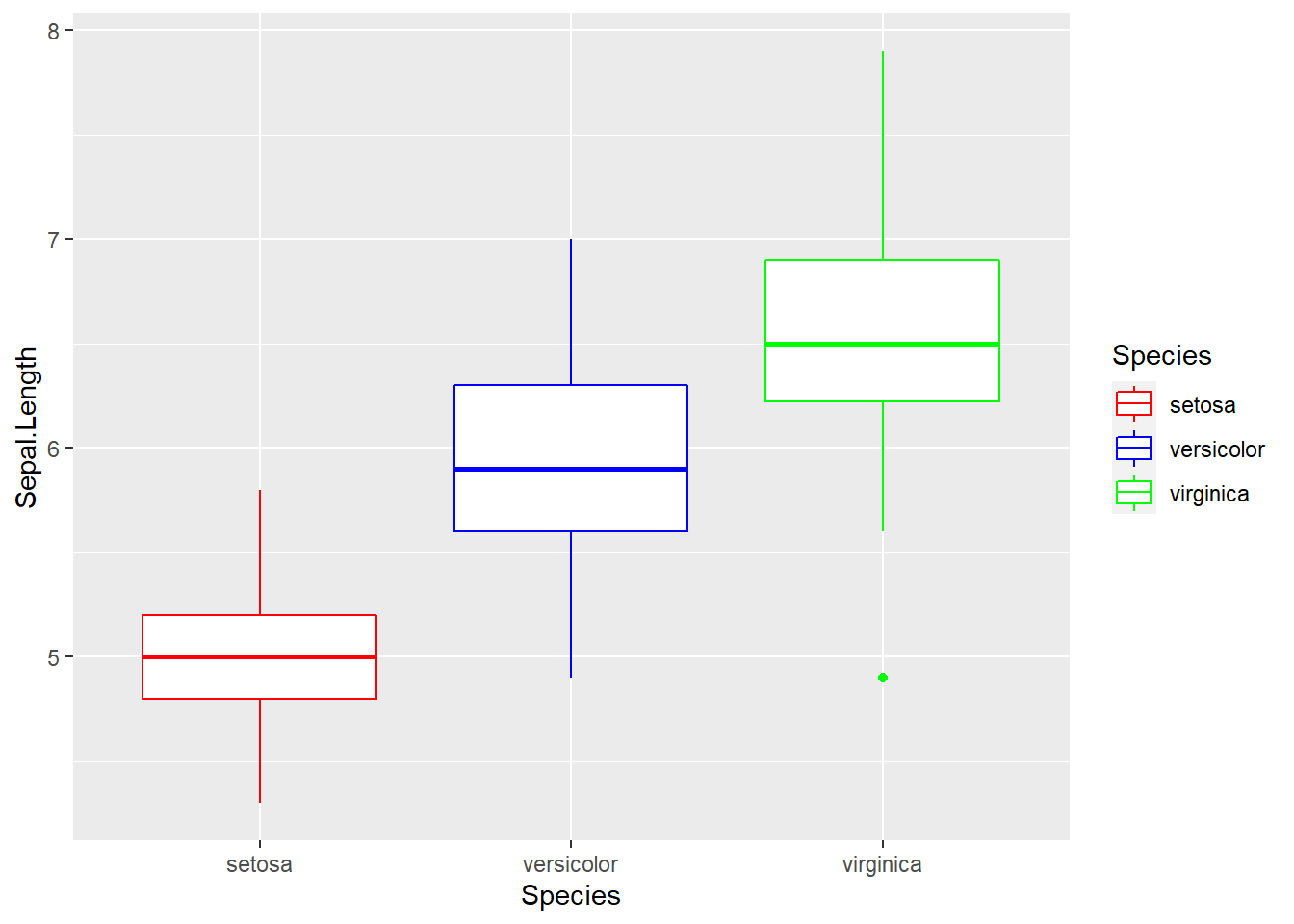

Secara default kategori pada legend akan diurutkan berdasarkan urutan level/kategori:

levels(iris$Species)

#> [1] "setosa"     "versicolor" "virginica"

Untuk mengurutkan kategori pada legend, kita dapat mengubah urutan level pada kolom kategori tersebut:

#order level
iris <- iris %>% 
  mutate(Species = factor(Species, levels = c("versicolor",
                                              "virginica",
                                              "setosa")))
#membuat visualisasi 
ggplot(data = iris, aes(x = Species,y = Sepal.Length))+
  geom_boxplot(aes(color = Species))+
  scale_color_manual(values = c("red","blue","green"))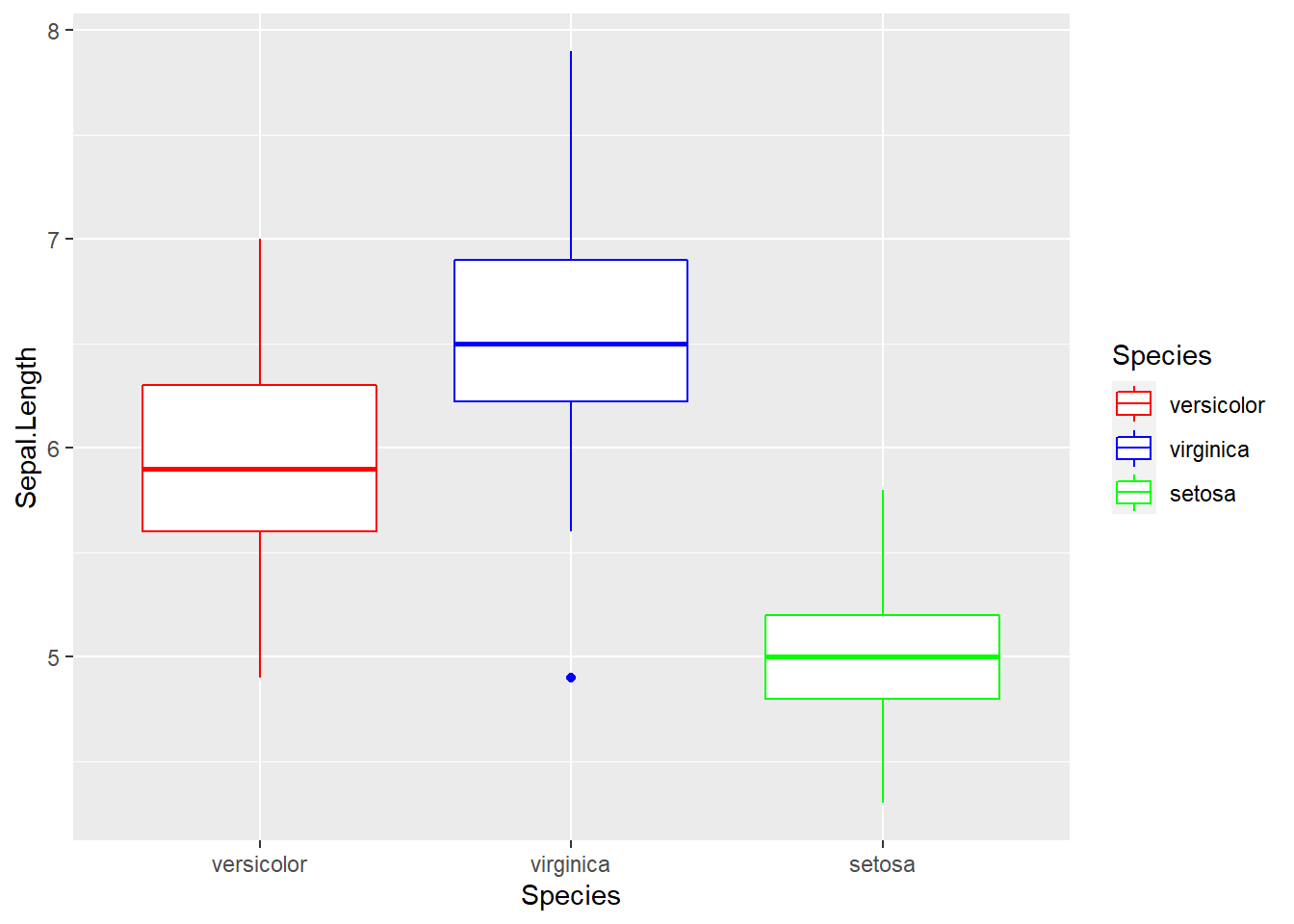

2.1.2.4 Bagaimana cara membuat lebih dari satu line pada satu grafik dengan menggunakan geom_line?

#>    market_A market_B       date
#> 1 100.00000 150.0000 2002-01-01
#> 2  92.31064 146.1417 2002-02-01
#> 3  82.61754 142.7523 2002-03-01
#> 4  84.71044 136.7259 2002-04-01
#> 5  66.96577 131.4398 2002-05-01
#> 6  65.70774 126.9375 2002-06-01

Untuk membuat grafik line dari dua variabel sekaligus, kita perlu melakukan manipulasi dari kedua variabel tersebut menjadi satu variabel dengan bantuan function pivot_longer() dari package tidyr. Data yang akan diperoleh sebagai berikut:

data_viz <- datline %>% 
            pivot_longer(cols = c(market_A,market_B),
            names_to = "market")
head(data_viz)

#> # A tibble: 6 x 3
#>   date       market   value
#>   <date>     <chr>    <dbl>
#> 1 2002-01-01 market_A 100  
#> 2 2002-01-01 market_B 150  
#> 3 2002-02-01 market_A  92.3
#> 4 2002-02-01 market_B 146. 
#> 5 2002-03-01 market_A  82.6
#> 6 2002-03-01 market_B 143.

Setelah data dimanipulasi, selanjutnya kita dapat melakukan visualisasi seperti biasa. Karena kita ingin membedakan grafik line berdasarkan kategori, kita bisa menggunakan parameter group untuk membedakan grafik line berdasarkan category.

ggplot(data = data_viz, aes(x = date,y = value, group = market)) +
  geom_line()

2.1.2.5 Bagaimana cara untuk menampilkan nilai (value) pada stacked bar?

Berikut ini merupakan data yang akan digunakan untuk visualisasi:

#>       year category freq
#> 1  2020-01        A  231
#> 2  2020-01        B  226
#> 3  2020-01        C  255
#> 4  2020-01        D  206
#> 5  2020-02        A  247
#> 6  2020-02        B  248
#> 7  2020-02        C  281
#> 8  2020-02        D  237
#> 9  2020-03        A  255
#> 10 2020-03        B  217
#> 11 2020-03        C  262
#> 12 2020-03        D  288
#> 13 2020-04        A  228
#> 14 2020-04        B  240
#> 15 2020-04        C  276
#> 16 2020-04        D  267

Untuk menampilkan value pada stack bar, kita dapat menambahkan function position_stack() pada geom_text dan juga sertakan label yang akan ditampilkan pada plot:

ggplot(dat_cat, aes(x = year,y = freq)) +
  geom_col(position = "stack",
           aes(fill = category))+
  geom_text(aes(label = freq), 
            position = position_stack(vjust = 0.5))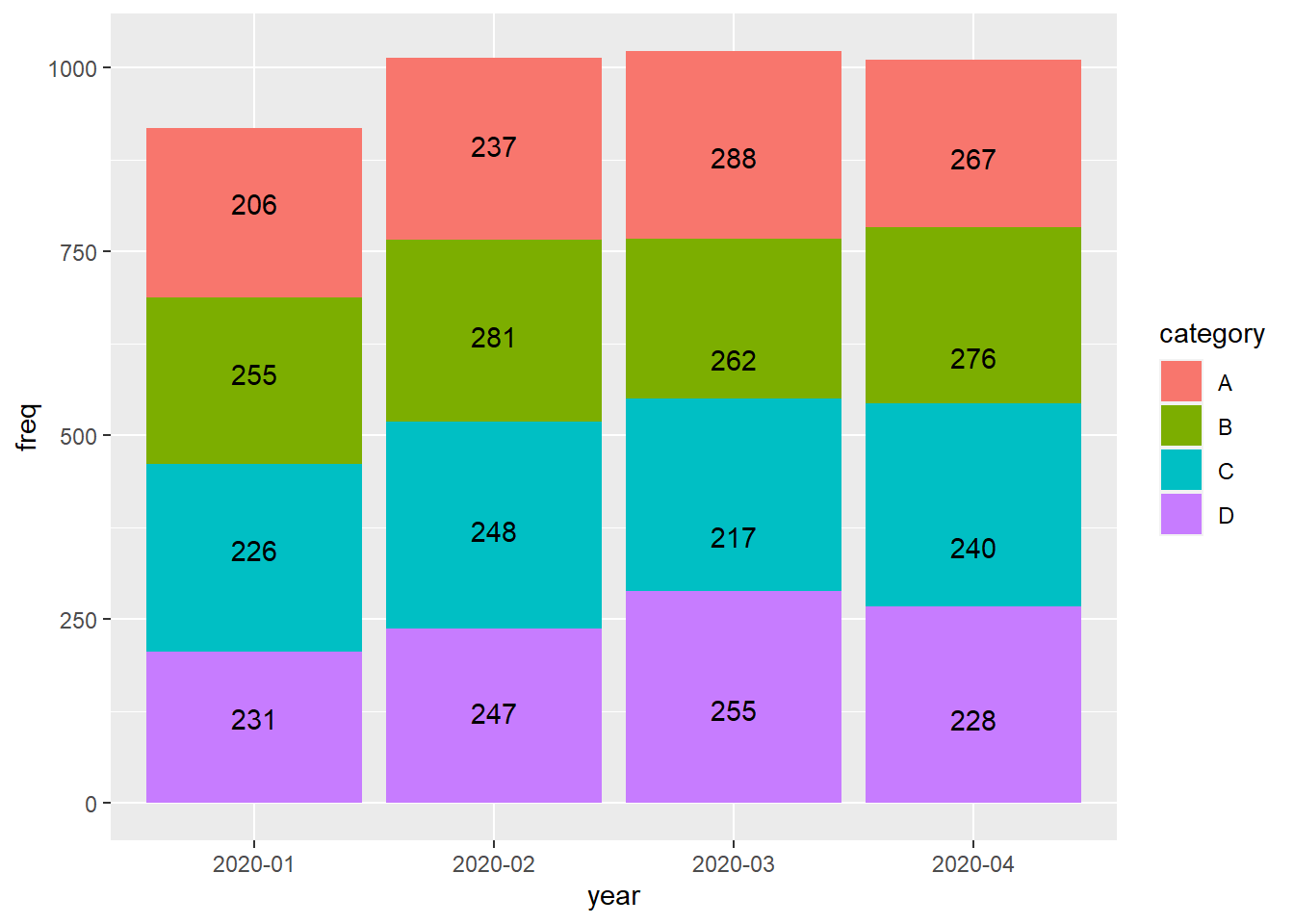

2.1.2.6 Bagaimana cara membuat secondary axis pada ggplot2?

#>             Timestamp air_temp
#> 1 2021-03-16 17:00:00     21.2
#> 2 2021-03-16 16:30:00     21.2
#> 3 2021-03-16 16:00:00     21.7
#> 4 2021-03-16 15:30:00     21.8
#> 5 2021-03-16 15:00:00     21.7
#> 6 2021-03-16 14:30:00     21.1

Penggunaan secondary axis pada ggplot2 diatur melalui function scale_y_continuous(), dengan menggunakan parameter sec.axis. Kita dapat menyesuaikan formula pada secondary axis tersebut pada parameter trans.

ggplot(data = weather, aes(x = Timestamp,y = air_temp))+
  geom_line()+
  scale_y_continuous(sec.axis = sec_axis(trans = ~.*5,
                                         name = "Relative Humidity [%]"))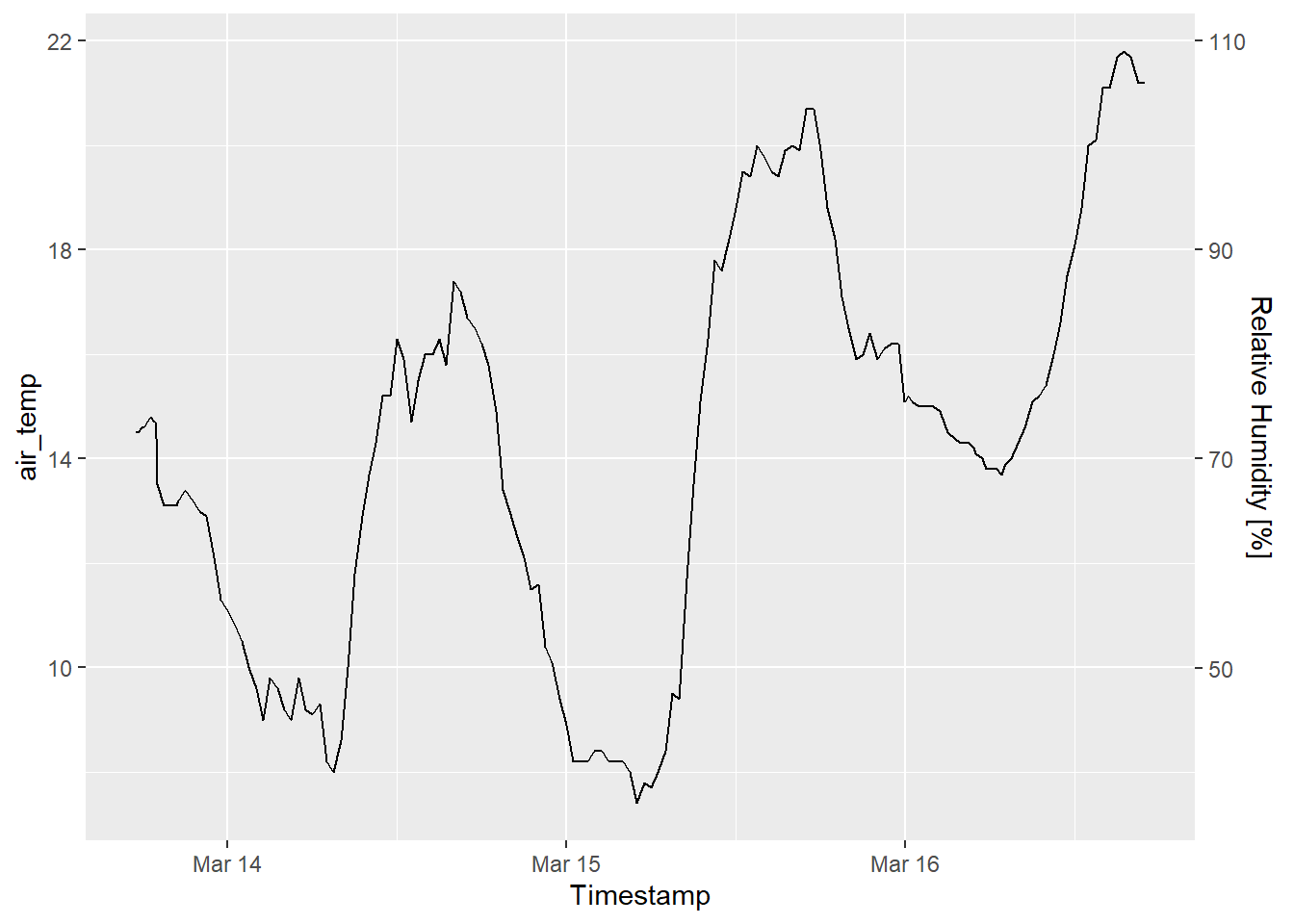

2.1.2.7 Bagaimana cara membuat multi row axis label pada ggplot?

#>   year quarter   profit
#> 1 2016      Q1 182.4233
#> 2 2016      Q2 205.6036
#> 3 2016      Q3 199.2379
#> 4 2016      Q4 234.0375
#> 5 2017      Q1 208.0940
#> 6 2017      Q2 216.1521

Untuk membuat multi axis pada ggplot, kita dapat menggunakan function annotate(). Pada function annotate() kita dapat menambahkah geom pada plot, namun tidak seperti geom lainnya yang memetakan data frame, melainkan untuk menyisipkan elemen vector seperti label text.

ggplot(data = dat_quarter, aes(x = interaction(year, quarter, lex.order = T),
                               y = profit, group = 1))+
  geom_line(colour = "blue")+
  annotate(geom = "text",
           x = seq_len(nrow(dat_quarter)),
           y = 126,
           label = dat_quarter$quarter, size = 4)+
  annotate(geom = "text",
           x = 2.5 + 4 *(0:4),
           y = 115,
           label = unique(dat_quarter$year),
           size = 6)+
  coord_cartesian(ylim = c(130,300),
                  expand = FALSE, 
                  clip = "off")+
  labs(title = "Total Quarterly Net Profits",
       y = NULL)+
    theme_minimal() +
  theme(plot.margin = unit(c(1, 1, 4, 1), "lines"),
        axis.title.x = element_blank(),
        axis.text.x = element_blank(),
        panel.grid.major.x = element_blank(),
        panel.grid.minor.x = element_blank())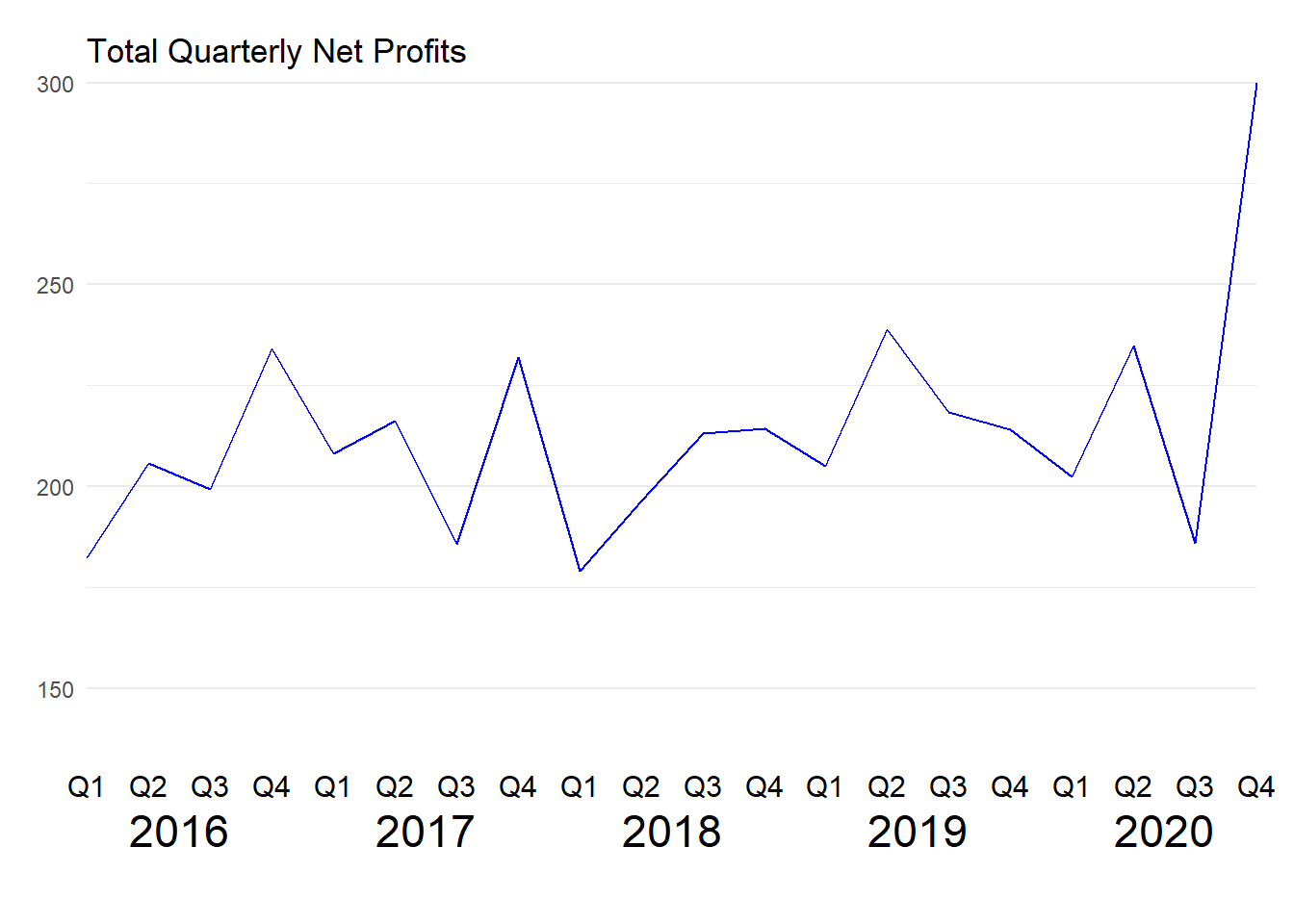

2.1.2.8 Bagaimana cara untuk membuat scatterplot dengan histogram marginal?

set.seed(100)
df <- data.frame(Var1 = rnorm(1000, 50, 10),
                 Var2 = rnorm(1000, 50,10))
head(df)

#>       Var1     Var2
#> 1 44.97808 60.97650
#> 2 51.31531 61.81037
#> 3 49.21083 55.87511
#> 4 58.86785 60.76173
#> 5 51.16971 61.36653
#> 6 53.18630 57.60293

Untuk membuat histogram marginal, kita dapat menggunakan function ggMarginal() dari package ggExtra. Kita dapat mengatur tipe grafik sesuai kebutuhan, tipe yang tersedia yaitu density, histogram, boxplot, violin, dan densigram.

p <- ggplot(data = df, aes(x = Var1,y = Var2))+
  geom_point()+
  theme_minimal()
ggExtra::ggMarginal(p, type = "histogram")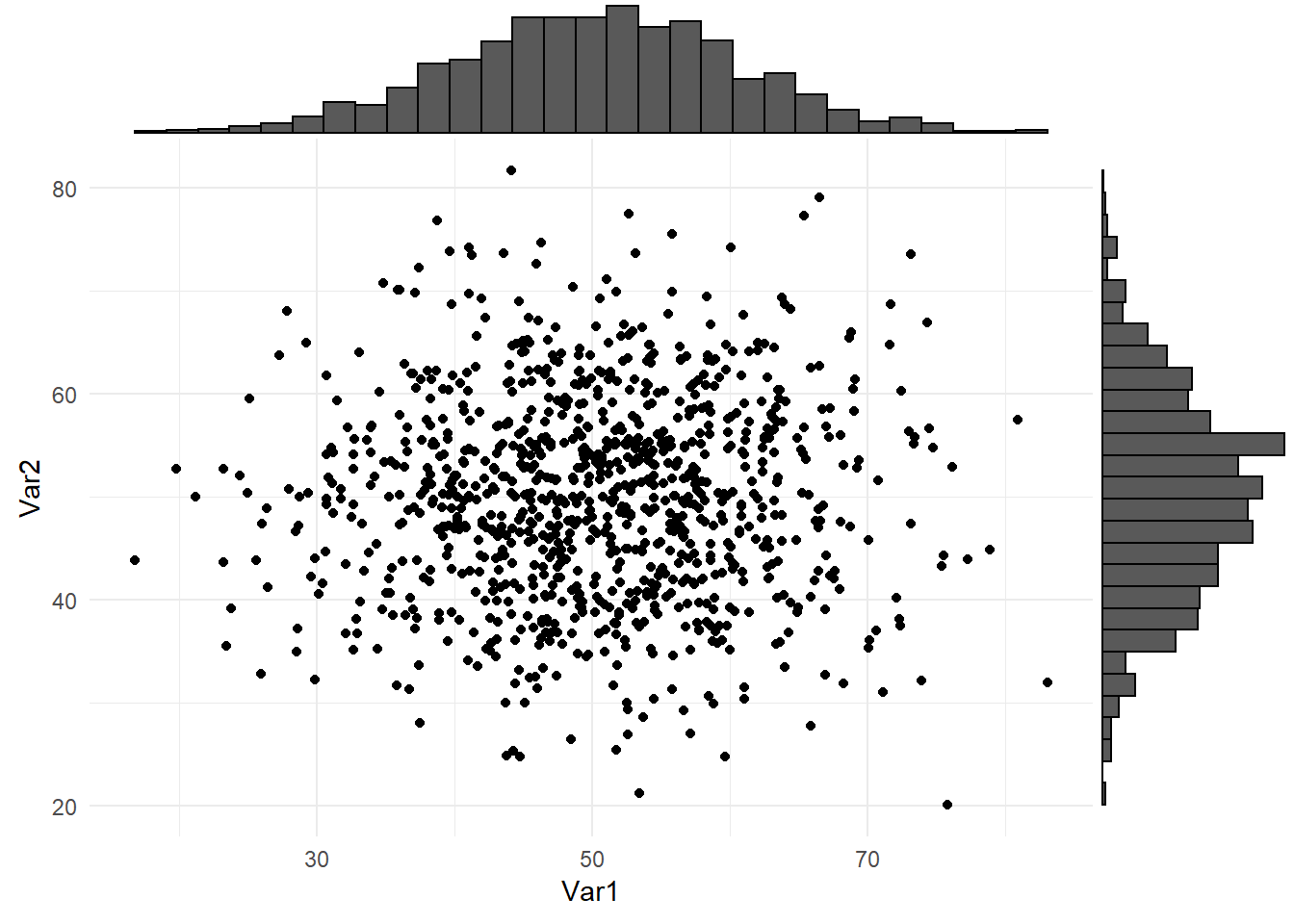

2.1.2.9 Bagaimana cara membuat spatial map menggunakan ggplot2?

Untuk membuat spatial map dengan ggplot2 kita bisa menggunakan geom_sf() sebagai berikut:

Data yang digunakan merupakan data default dari salah satu package R, yaitu rnaturalearth. Untuk menarik data tersebut dapat mengunakan fungsi ne_countries().

library(ggplot2)
library(sf)
library(rnaturalearth)

world_data <- ne_countries(scale = "medium", returnclass = "sf")
class(world_data)

#> [1] "sf"         "data.frame"

Spatial map yang akan dibuat menggambarkan total poplasi penduduk untuk setiap negara.

new.world_data <- world_data[(!is.na(world_data$pop_est)), ] 

ggplot(data = new.world_data) +
  geom_sf(color = "black", aes(fill = pop_est)) +
  labs(title = paste("World Map:", length(unique(new.world_data$name)), "countries"),
       x = "Longitude",
       y = "Latitude",
       fill = "Estimate Total Population") +
  scale_fill_gradient(low = "grey", high = "red") +
  theme_minimal()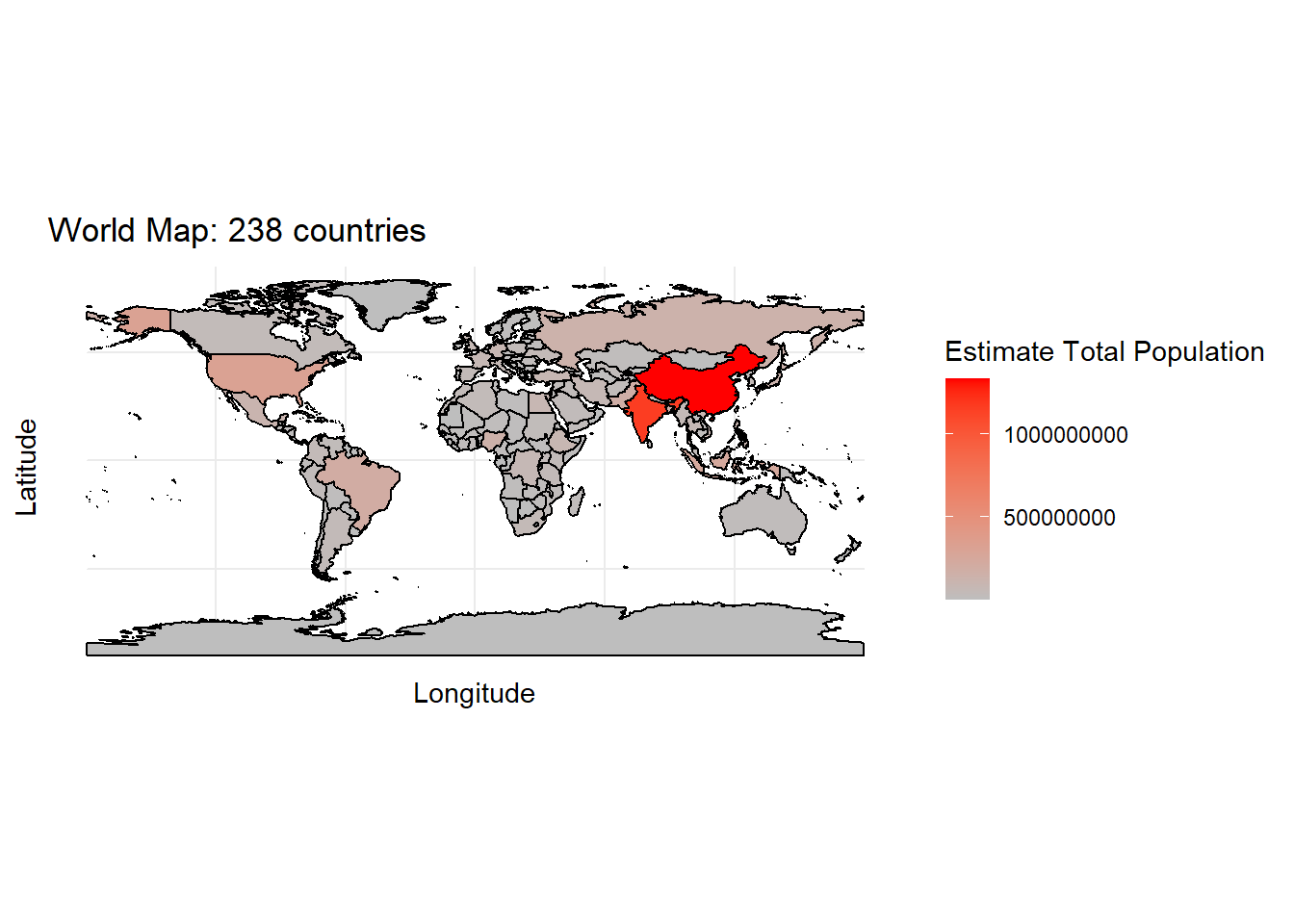

Membuat spatial map di atas menjadi interaktif (interactive spatial map)

# membuat kolom baru yang berisi teks yang akan ditampilkan saat dilakukan hovering
new.world_data <- new.world_data %>% 
  mutate(text = glue("Country: {name}
                      Total Population: {pop_est}")) 

# melakukan assignment spatial map ke dalam objek baru
interactive_map <- ggplot(data = new.world_data) +
  geom_sf(color = "black", aes(fill = pop_est, text = text)) +
  labs(title = paste("World Map:", length(unique(new.world_data$name)), "countries"),
       x = "Longitude",
       y = "Latitude",
       fill = "Estimate Total Population") +
  scale_fill_gradient(low = "grey", high = "red") +
  theme_minimal()

ggplotly(interactive_map, tooltip = "text")

2.1.3 Scale

2.1.3.1 Bagaimana cara memberi big mark pada axis plot?

untuk memberikan big mark pada axis dapat dibantu dengan package scales

ggplot(vids3, aes(views, likes)) +
  geom_point(aes(color = category_id))  +
  scale_y_continuous(labels = comma)+
  scale_x_continuous(labels = comma)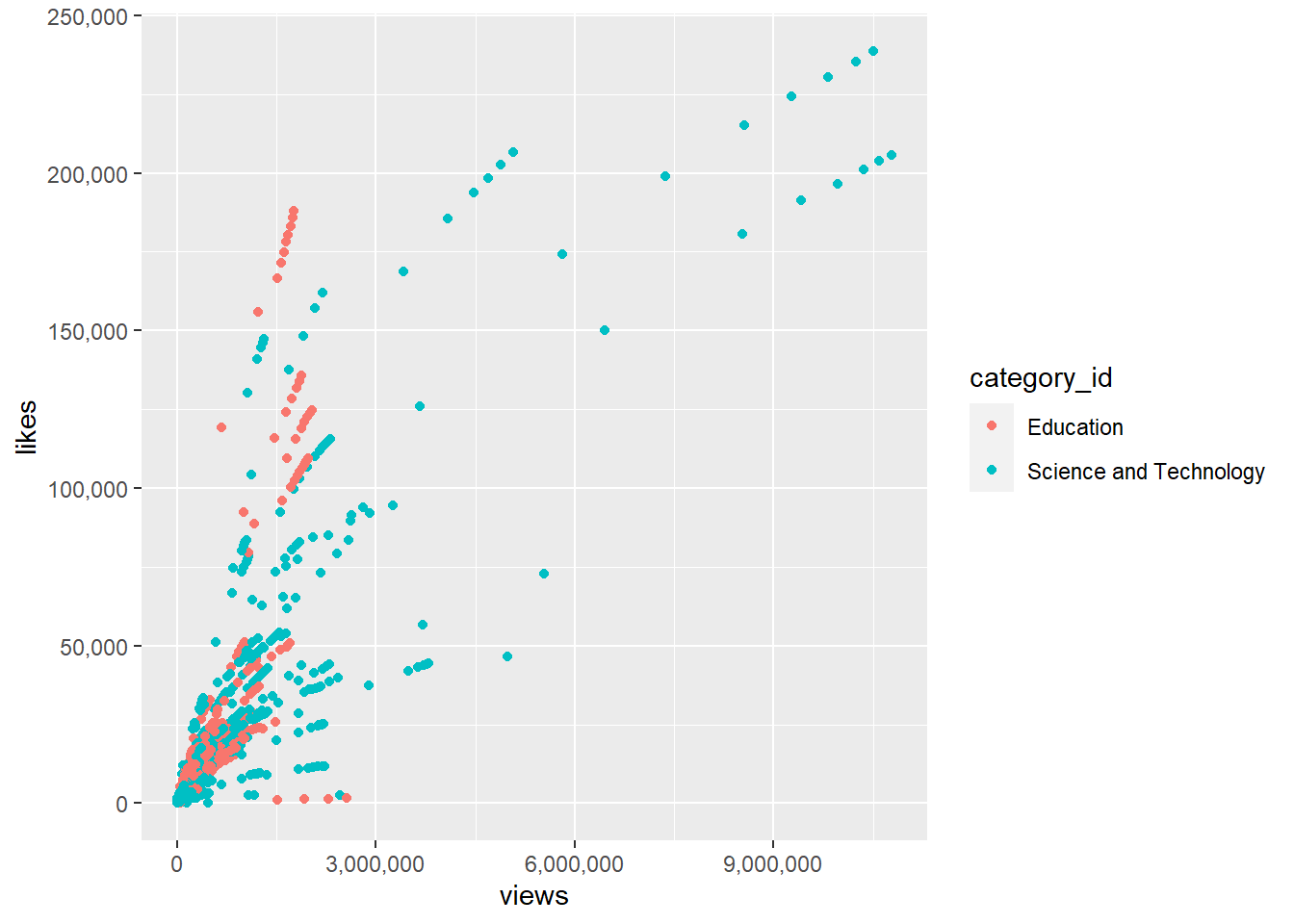

2.1.3.2 Apakah pengaturan label baik pada sumbu x ataupun y dapat dilakukan secara terpisah? misal kita ingin memeberikan label ribuan (1 ribu, 2 ribu, dst). Namun, pada angka 0 tidak ingin diikuti oleh “ribuan”.

Tidak bisa dilakukan secara terpisah, karena parameter labels pada fungsi scale_y_continous akan menambahkan satuan pada semua nilai label. Alternatif lain yang dapat dilakukan adalah membuat judul (title) pada sumbu x ataupun y dengan disertai oleh satuan. Misal, “Dislikes (Ribu)”, kemudian membuat skalanya menjadi lebih kecil (50000 menjadi 50 saja).

2.1.3.3 Bagaimana mengatasi axis yang memiliki satuan besar seperti berikut ini?

ggplot(data_agg, aes(x = belanja_daerah, y = reorder(daerah, belanja_daerah))) +
  geom_col(aes(fill = belanja_daerah)) +
  scale_fill_continuous(low = "orange", high = "red") +
  guides(fill = FALSE) +
  labs(
    title = "10 Daerah dengan Realisasi Belanja Daerah tertinggi 2018",
    x = NULL,
    y = NULL
  ) +
  theme_minimal()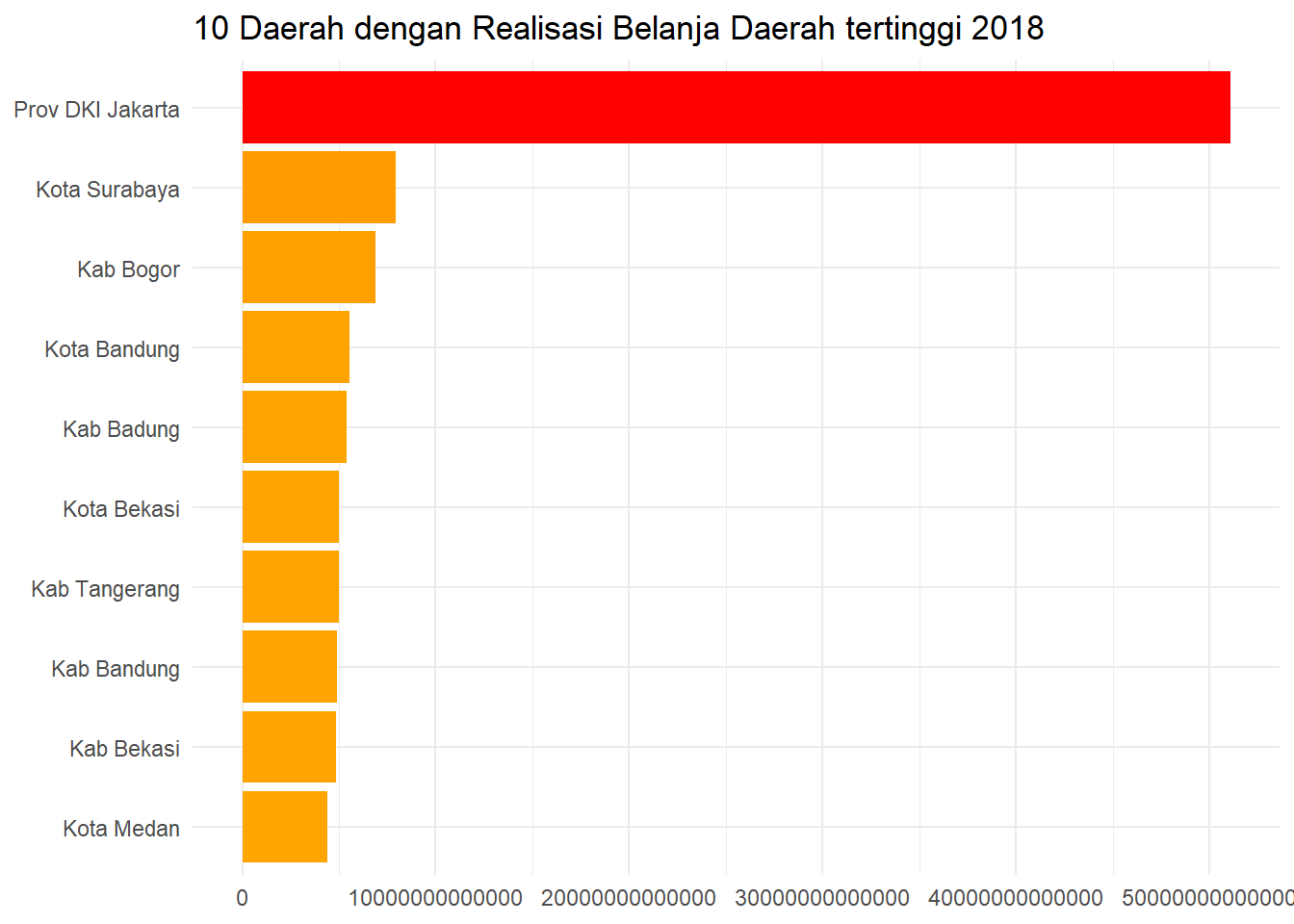

Ketika kita melakukan visualisasi, adanya satuan axis yang cukup banyak tersebut dapat menyulitkan audience dalam memahami informasi pada grafik tersebut. Kita dapat mengatur scale axis pada plot tersebut dengan bantuan package scales. Berikut ini kita akan membuat object yang berisikan function label untuk merapihkan axis text pada plot:

label_rupiah <- label_dollar(scale = 1e-9, prefix = "Rp ", suffix = " M")

Selanjutnya, aplikasikan label tersebut pada function scale_y_continuous()

ggplot(data_agg, aes(x = belanja_daerah, y = reorder(daerah, belanja_daerah))) +
  geom_col(aes(fill = belanja_daerah)) +
  scale_x_continuous(labels = label_rupiah)+
  scale_fill_continuous(low = "orange", high = "red") +
  guides(fill = FALSE) +
  labs(
    title = "10 Daerah dengan Realisasi Belanja Daerah tertinggi 2018",
    x = NULL,
    y = NULL
  ) +
  theme_minimal()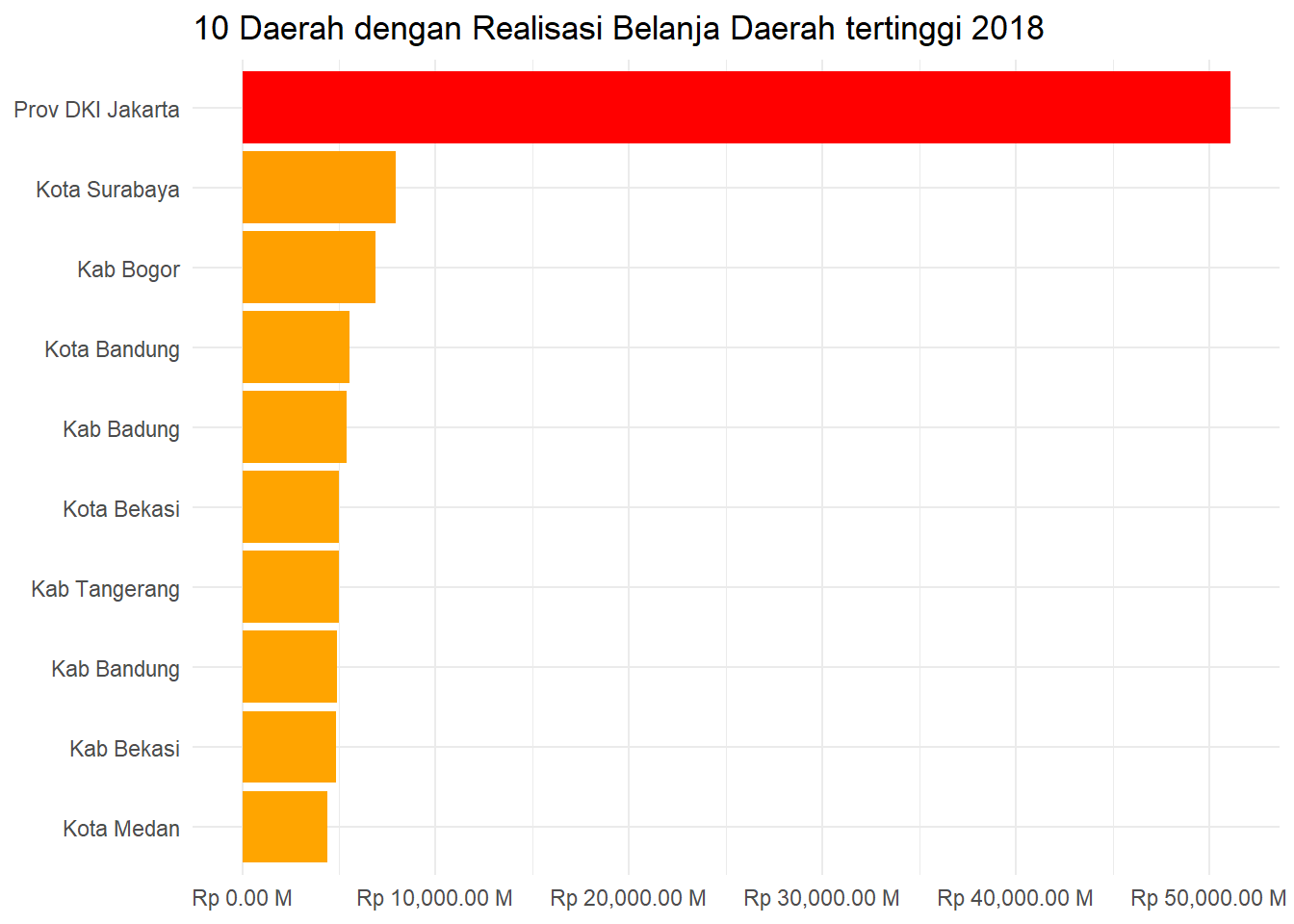

Setelah diaplikasikan label pada axis text terlihat lebih mudah dipahami informasi yang disampaikan pada grafik tersebut.

2.1.3.4 Bagaimana cara untuk mewarnai dan memberi label pada bar tertentu pada plot?

Misalkan, pada data top 10 trending channel akan dibentuk bar plot dan kita akan membedakan warna pada top 3 channel tersebut. Untuk pewarnaan dari top 3 channel kita memerlukan geom_col() tambahan yang berisi 3 data awal yang akan ditampilkan, begitupun pada geom_label() pada parameter data kita define observasi mana saja yang ingin diberikan label.

#> # A tibble: 10 x 2
#>    channel_title                          total
#>    <chr>                                  <int>
#>  1 Refinery29                                31
#>  2 The Tonight Show Starring Jimmy Fallon    30
#>  3 Vox                                       29
#>  4 TheEllenShow                              28
#>  5 Netflix                                   27
#>  6 NFL                                       25
#>  7 ESPN                                      24
#>  8 Jimmy Kimmel Live                         24
#>  9 The Late Show with Stephen Colbert        22
#> 10 Late Night with Seth Meyers               21

ggplot(data = vids.top,mapping = aes(x = total,
                                     y = reorder(channel_title,total)))+
  geom_col(fill = "skyblue")+
  geom_col(data = vids.top[1:3,], fill = "navy")+
  geom_label(data = vids.top[1:3,],
             mapping = aes(label = total))+
  labs(title = "Top 10 Trending Channel in US",
       subtitle = "Based on Video Count",
       x = "",
       y = "Video Count")+
  theme_minimal()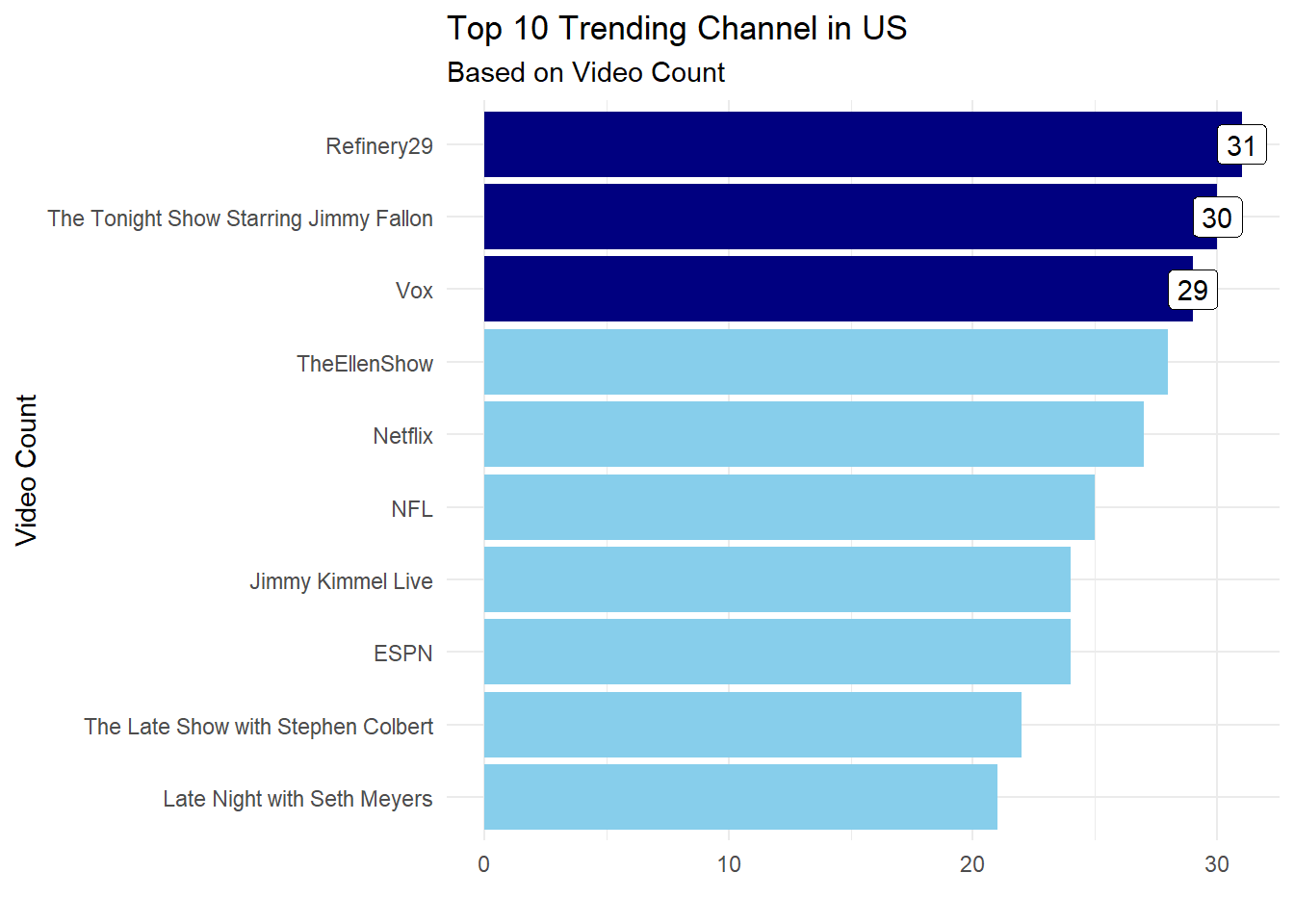

2.1.4 Theme

2.1.4.1 Secara umum elemen-elemen apa saja yang dapat diatur/disesuaikan pada fungsi theme()?

Berikut adalah gambaran elemen-elemen apa saja yang dapat diatur/disesuaikan dengan fungsi theme()

• plot.background: digunakan untuk menyesuaikan/mengatur warna background plot/kanvas. Digunakan dengan menambahkan parameter element_rect untuk menyesuaikan warna background yang diinginkan (colour).

• plot.margin: digunakan untuk memberi jarak antara kanvas utuh dengan kotak tempat plot berada. Digunakan dengan menambahkan parameter unit.

• plot.title: digunakan untuk menyesuaikan/mengatur elemen yang berkaitan dengan judul plot. Digunakan dengan menambahkan parameter element_text() untuk mengatur spesifikasi tulisan yang diinginkan mulai dari ukuran (size), rata kiri-kanan/alignment (hjust), cetak tebal/miring (face), dll.

• plot.subtitle: digunakan untuk menyesuaikan/mengatur elemen yang berkaitan dengan sub-judul plot. Digunakan dengan menambahkan parameter element_text() untuk mengatur spesifikasi tulisan yang diinginkan mulai dari ukuran (size), rata kiri-kanan/alignment (hjust), cetak tebal/miring (face), dll.

• axis.title.x: digunakan untuk menyesuaikan/mengatur elemen yang berkaitan dengan judul pada bagian sumbu x (horizontal). Digunakan dengan menambahkan parameter element_text() untuk mengatur spesifikasi tulisan yang diinginkan mulai dari ukuran (size), rata kiri-kanan/alignment (hjust), cetak tebal/miring (face), dll.

• axis.text.x: digunakan untuk menyesuaikan/mengatur elemen yang berkaitan dengan tulisan pada bagian sumbu x (horizontal). Digunakan dengan menambahkan parameter element_text() untuk mengatur spesifikasi tulisan yang diinginkan mulai dari ukuran (size), rata kiri-kanan/alignment (hjust), cetak tebal/miring (face), dll.

• axis.title.y: kegunaanya sama persis seperti parameter axis.title.x, perbedaanya adalah digunakan pada sumbu y (vertikal).

• axis.text.y: kegunaanya sama persis seperti parameter axis.text.x, perbedaanya adalah digunakan pada sumbu y (vertikal).

• panel.background: digunakan untuk mengubah warna panel background, dengan menambahkan parameter element_rect untuk menyesuaikan warna panel background yang diinginkan (colour).

• panel.grid: digunakan untuk mengubah tampilan garis kisi (grid) pada plot. Digunakan dengan menambahkan parameter element_line untuk mengatur warna garis (colour), tipe garis (linetype), ukuran garis (size), dll.

• plot.caption: digunakan untuk menyesuaikan/mengatur elemen yang berkaitan dengan caption plot (tulisan tambahan yang terletak pada bagian bawah plot). Digunakan dengan menambahkan parameter element_text() untuk mengatur spesifikasi tulisan yang diinginkan mulai dari ukuran (size), rata kiri-kanan/alignment (hjust), cetak tebal/miring (face), dll.

• legend.title: digunakan untuk menyesuaikan/mengatur elemen yang berkaitan dengan judul legend. Digunakan dengan menambahkan parameter element_text() untuk mengatur spesifikasi tulisan yang diinginkan mulai dari ukuran (size), rata kiri-kanan/alignment (hjust), cetak tebal/miring (face), dll.

• legend.background: digunakan untuk mengubah warna background legend, dengan menambahkan parameter element_rect untuk menyesuaikan warna panel background yang diinginkan (colour).

• legend.position: digunakan untuk mengatur letak/posisi legend pada plot, digunakan dengan menambahakan parameter none, left, right, bottom, dan top

• legend.text: digunakan untuk menyesuaikan/mengatur elemen yang berkaitan dengan tulisan pada bagian legend. Digunakan dengan menambahkan parameter element_text() untuk mengatur spesifikasi tulisan yang diinginkan mulai dari ukuran (size), rata kiri-kanan/alignment (hjust), cetak tebal/miring (face), dll.

2.1.4.2 Bagaimana cara mengatur posisi legend secara manual (selain menggunakan position default “none”, “left”, “right”, “bottom”, dan “top”) supaya posisinya berada di dalam kanvas plotnya?

Untuk mengatur posisi legend secara manual dapat menambahakan parameter legend.position pada theme seperti berikut ini:

vids3 <- vids %>% 
  select(channel_title, category_id, views, likes) %>% 
  filter(category_id %in% c("Education", "Science and Technology"))

theme_algoritma <- theme(legend.background = element_rect(color="white", fill="#263238"),
           plot.subtitle = element_text(size=6, color="white"),
           panel.background = element_rect(fill="#dddddd"),
           panel.border = element_rect(fill=NA),
           panel.grid.minor.x = element_blank(),
           panel.grid.major.x = element_blank(),
           panel.grid.major.y = element_line(color="darkgrey", linetype=2),
           panel.grid.minor.y = element_blank(),
           plot.background = element_rect(fill="#263238"),
           text = element_text(color="white"),
           axis.text = element_text(color="white"))

ggplot(vids3, aes(views, likes)) +
  geom_point(aes(color = category_id)) +
  geom_smooth(method = "lm", color = "darkgrey") +
  labs(title = "Likes VS Views",
       subtitle = "Category: Education & Science and Technology",
       x = "Views",
       y = "Likes",
       caption = "Source: Algoritma",
       col = "Category") +
  scale_color_manual(values = c("red", "black")) +
  theme(legend.position = c(0.85, 0.15)) +
  theme_algoritma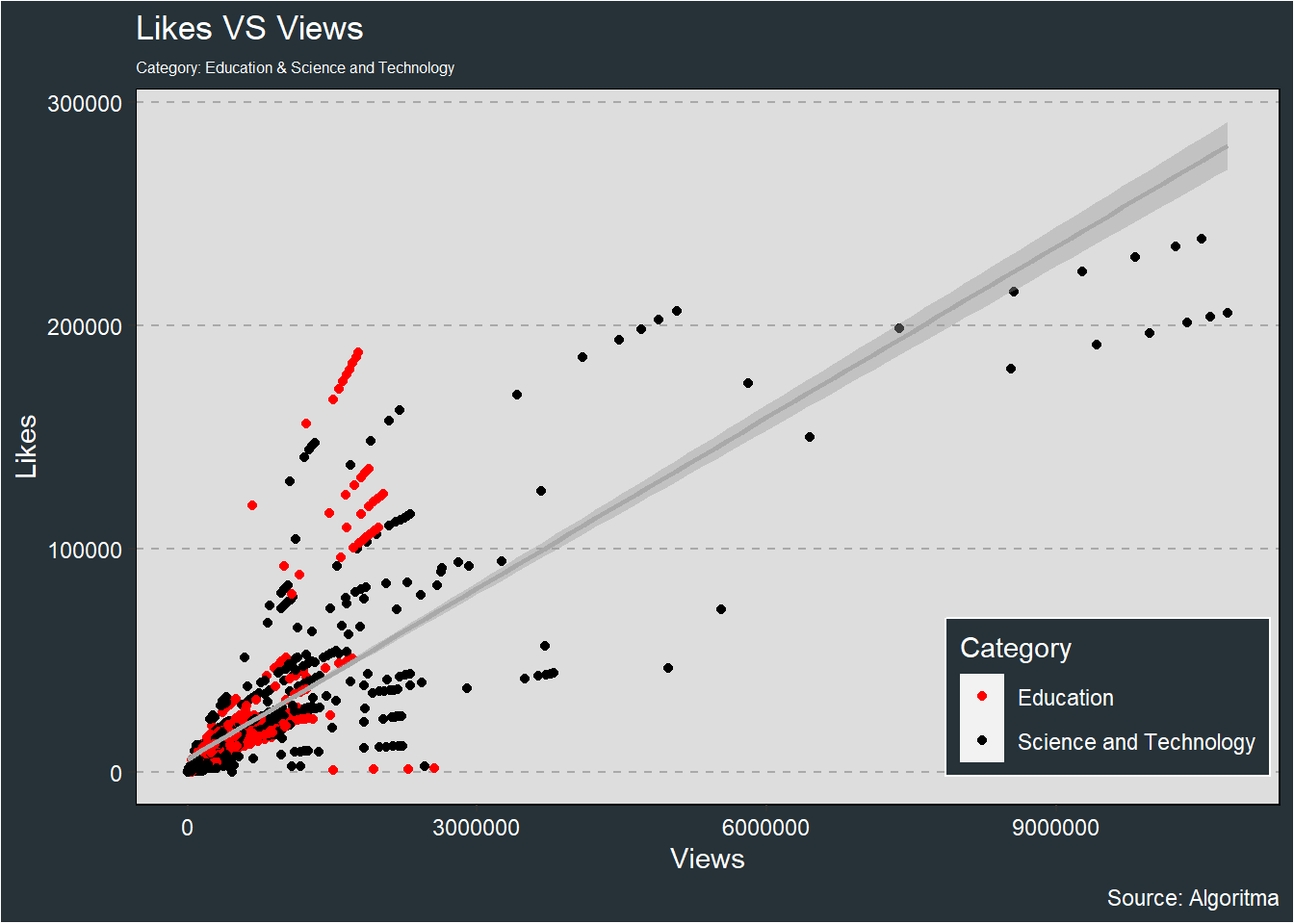

2.2 Interactive plotting

2.2.0.1 Contoh penggunaan echarts4r untuk beberapa plot sederhana

library(echarts4r)

• Line Plot

vids2 <-  vids %>% 
  select(trending_date, channel_title, category_id) %>% 
  filter(category_id %in% c("Education", "Science and Technology"),) %>% 
  group_by(trending_date, category_id) %>% 
  summarise(total.video = n()) %>% 
  ungroup()

vids2 %>% 
  group_by(category_id) %>% 
  e_charts(trending_date) %>% 
  e_line(total.video) %>% 
  e_legend(F) %>% 
  e_title("Trend Total Video Trending based on Category")

• Area charts

vids2 %>% 
  group_by(category_id) %>% 
  e_charts(trending_date) %>% 
  e_area(total.video) %>% 
  e_legend(F) %>% 
  e_title("Trend Total Video Trending based on Category")

• Bar plot

vids1 %>% 
  e_charts(channel_title) %>% 
  e_bar(total.likes) %>%
  e_legend(F) %>% 
  e_title("Top 5 Channel based on Total Likes")

• Scatter plot

vids3 %>% 
  group_by(category_id) %>% 
  e_charts(views) %>% 
  e_scatter(likes) %>%
  e_title("Likes VS Views")

• Heatmap

retail <- read.csv("data/02-DVIP/retail.csv")

retail.agg1 <- retail %>% 
  group_by(Sub.Category, Ship.Mode) %>% 
  summarise(Sales = sum(Sales)) %>% 
  ungroup()

retail.agg1 %>% 
  e_charts(Ship.Mode) %>% 
  e_heatmap(Sub.Category, Sales) %>% 
  e_visual_map(Sales) %>% 
  e_title("Heatmap") %>% 
  e_legend(type = c("scroll"))

• Treemap

retail.agg2 <- retail %>% 
  group_by(Segment, Ship.Mode) %>% 
  summarise(jumlah.customer = n_distinct(Customer.ID)) %>% 
  ungroup()

retail.agg2 %>% 
  e_charts() %>% 
  e_treemap(Segment, Ship.Mode, jumlah.customer) %>% 
  e_title("Treemap charts")

2.2.0.2 Bagaimana cara membuat e-charts menjadi interaktif?

vids1 %>% 
  e_charts(channel_title) %>% 
  e_bar(total.likes) %>%
  e_legend(F) %>% 
  e_title("Top 5 Channel based on Total Likes") %>% 
  e_tooltip(trigger = "item", 
            axisPointer = list(type = "cross"))

2.2.0.3 Contoh penggunaan highcharter untuk beberapa plot sederhana:

library(highcharter)

• Scatter plot

hchart(vids3, "scatter", hcaes(x = views, y = likes, group = category_id)) %>% 
  hc_title(text = "Likes VS Views") %>% 
  hc_subtitle(text = "Category: Education & Science and Technology")

• Bar Plot

hchart(vids1, "column", hcaes(x = channel_title, y = total.likes)) %>% 
  hc_title(text = "Top 5 Channel based on Total Likes") %>% 
  hc_subtitle(text = "Category: Education & Science and Technology")

• Line Plot

hchart(vids2, "line", hcaes(x = trending_date, y = total.video, group = category_id)) %>% 
  hc_title(text = "Trend Total Video Trending based on Category")

2.2.0.4 Bagaimana cara untuk menampilkan pop-up informasi dari grafik?

Untuk membuat plot menjadi interactive, kita dapat menggunakan package glue dan plotly.

#> # A tibble: 10 x 2
#>    daerah           belanja_daerah
#>    <chr>                     <dbl>
#>  1 Prov DKI Jakarta 51066081000000
#>  2 Kota Surabaya     7912409000000
#>  3 Kab Bogor         6875742000000
#>  4 Kota Bandung      5541718000000
#>  5 Kab Badung        5413936000000
#>  6 Kota Bekasi       4982355000000
#>  7 Kab Tangerang     4981819000000
#>  8 Kab Bandung       4911936000000
#>  9 Kab Bekasi        4846112000000
#> 10 Kota Medan        4395825000000

Berikut ini kita akan membuat kolom baru bernama tooltip, gunakan function glue() untuk mendefinisikan informasi yang akan ditampilkan. Pada variable “belanja_daerah” yang ditampilkan diberikan function label_rupiah() yang sudah dibuat pada pembahasan sebelumnya agar tampilan menjadi lebih rapih.

# Prepare data for visualization
data_viz <- data_agg %>% 
  mutate(tooltip = glue("Belanja daerah: {label_rupiah(belanja_daerah)}"))
head(data_viz)

#> # A tibble: 6 x 3
#>   daerah           belanja_daerah tooltip                       
#>   <chr>                     <dbl> <glue>                        
#> 1 Prov DKI Jakarta 51066081000000 Belanja daerah: Rp 51,066.08 M
#> 2 Kota Surabaya     7912409000000 Belanja daerah: Rp 7,912.41 M 
#> 3 Kab Bogor         6875742000000 Belanja daerah: Rp 6,875.74 M 
#> 4 Kota Bandung      5541718000000 Belanja daerah: Rp 5,541.72 M 
#> 5 Kab Badung        5413936000000 Belanja daerah: Rp 5,413.94 M 
#> 6 Kota Bekasi       4982355000000 Belanja daerah: Rp 4,982.36 M

Untuk memberikan hovertext pada setiap bar, kita dapat gunakan parameter text dan isi dengan nama kolom yang akan ditampilkan. Selanjutkan, gunakan function ggplotly() untuk membuat plot menjadi interactive, parameter tooltip digunakan untuk mengatur informasi yang akan ditampilkan. Secara default, dia akan menampilkan semua informasi yang ada pada parameter aes, ketika kita define “text” artinya kita akan menampilkan informasi dari parameter text.

# Visualization
p <- ggplot(data_viz, aes(x = belanja_daerah, y = reorder(daerah, belanja_daerah))) +
  geom_col(aes(fill = belanja_daerah, text = tooltip)) +
  scale_x_continuous(labels = label_rupiah) +
  scale_fill_continuous(low = "orange", high = "red") +
  guides(fill = FALSE) +
  labs(
    title = "10 Daerah dengan Realisasi Belanja Daerah tertinggi 2018",
    x = NULL,
    y = NULL
  ) +
  theme_minimal()

ggplotly(p, tooltip = "text")

2.2.0.5 Apakah plotly juga dapat diatur/disesuaikan secara terpisah dari ggplot2?

Bisa, berikut beberapa contoh pengaturan pada plotly:

• Menghapus logo plotly pada mode bar

ggplotly(p, tooltip = "text") %>% 
  config(displaylogo = F) 

• Menghapus semua button (termasuk logo plotly) pada mode bar

ggplotly(p, tooltip = "text") %>% 
  config(displayModeBar = F) 

• Range selector

ggplotly(p, tooltip = "text") %>% 
  config(displayModeBar = F) %>% 
  rangeslider()

• Scroll with pan mode for zooming

ggplotly(p, tooltip = "text") %>% 
  config(displayModeBar = F, scrollzoom = T) %>% 
  layout(dragmode = "pan")

2.3 Leaflet

Kunjungi halaman berikut untuk Section Leaflet.

Bab 3 Practical Statistics

3.1 Statistika Deskriptif

3.1.1 Kekurangan nilai rata-rata (mean) adalah sensitif terhadap data ekstrim (outlier). Apakah kekurangan dari median?

• Median jarang digunakan dalam inferensial statistik karena tidak melibatkan semua data, sedangkan dalam mengambil keputusan dengan menggunakan tes/uji statistik semua data harus dilibatkan.
• Sebenarnya mean dan median bukan merupakan sesuatu yang harus dipilih. Keduanya bisa saja digunakan dalam proses eksplorasi data. Ketika kita melihat ringkasan dari data dan ternyata nilai mean jauh berbeda dengan nilai mediannya, maka hal tersebut dapat dijadikan salah satu indikator adanya outlier.

3.1.2 Apakah modus dapat digunakan untuk data bertipe numerik?

Bisa, hanya saja informasi yang diperoleh kurang representatif pada data bertipe numerik kontinu (desimal).

3.1.3 Apakah bisa menggunakan nilai mutlak/absolut saat menghitung variance, sebagai pengganti kuadrat?

Apabila menggunakan nilai mutlak/absolut saat menjumlahkan jarak dari setiap observasi ke pusat data (mean), maka ukuran tersebut disebut sebagai mean absolute deviation (rata-rata absolut deviasi).

$$\frac{\sum |x-\overline{x}|}{n}$$

3.1.4 Saat menghitung variance, kita menggunakan nilai mean sebagai pusat datanya. Ketika terdapat outlier, bukankah lebih tepat jika pusat datanya menggunakan median untuk menghitung variance?

Sesuai rumus variance, pusat data yang digunakan adalah mean. Tidak masalah walaupun terdapat outlier, karena nilai variance juga akan semakin membesar. Hal tersebut menunjukkan bahwa data kita semakin beragam/bervariasi karena adanya outlier.

3.1.5 Bagaimana menentukan suatu observasi merupakan outlier secara objektif?

Salah satu cara yang dapat digunakan untuk menentukan suatu observasi merupakan outlier/tidak adalah dengan menggunakan boxplot (melihat apakah suatu observasi berada di luar interval batas bawah (Q1 - 1.5 IQR) dan batas atas (Q3 + 1.5 IQR))

3.1.6 Apakah terdapat korelasi/keterkaitan antara mean dengan standar deviasi?

Tidak ada, karena mean adalah nilai yang menggambarkan pusat data (nilai yang merangkum keseluruhan data). Sedangkan, standar deviasi adalah nilai yang mengambarkan persebaran data (apakah data cenderung bervariasi/beragam)

3.1.7 Apakah pada R terdapat fungsi yang dapat digunakan untuk menentukan apakah dua variabel numerik memiliki hubungan linier atau tidak?

Kita dapat menggunakan fungsi cor() untuk menghitung nilai korelasi dan cor.test() untuk melakukan tes/uji statistik untuk mengetahui apakah dua variabel numerik saling berhubungan linier atau tidak dengan hipotesis sebagai berikut:

• H0: Nilai korelasi = 0, berarti antara x dan y tidak memiliki hubungan linier
• H1: Nilai korelasi != 0, berarti antara x dan y memiliki hubungan linier

3.1.8 Apa fungsi yang digunakan untuk menghitung nilai- rata-rata geometrik dan terboboti pada R?

Kita dapat menggunakan fungsi geometric.mean() dan weighted.mean(), untuk lebih jelasnya dapat membaca dokumentasi pada link berikut:

• Geometric Mean in R (2 Examples)
• weighted.mean

3.1.9 Apa yang dimaksud dengan outlier? Jelaskan!

Observasi yang nilainya sangat jauh berbeda dengan observasi lainnya baik sebagai variabel tunggal ataupun kombinasi.

3.2 Statistika Inferensial

3.2.1 Apabila data populasi tidak berdistribusi normal, apakah berpengaruh terhadap sampling rata-rata?

Central Limit Theorem (CLT) menyatakan bahwa apapun bentuk distribusi data populasi, ketika dilakukan sampling dengan jumlah yang cukup banyak dan dilakukan berulang kali, maka distribusi rata-rata sampel akan mendekati distribusi normal. Sehingga, ketika data populasi tidak berdistribusi normal, tidak akan berpengaruh terhadap distribusi rata-rata sampel selama jumlah sampel cukup (umumnya di atas 30) dan dilakukan berulang kali.

3.2.2 Contoh kegunaan Probability Mass Function dalam dunia nyata?

• Mengetahui proporsi jumlah produk yang cacat dalam proses produksi
• Mengetahui proporsi nasabah yang pengajuan pinjamannya disetujui
• Mengetahui distribusi banyaknya pelanggan yang datang ke toko setiap jamnya
• Mengetahui distribusi antrian di setiap kasir pada suatu toko

3.2.3 Dalam ilmu statistik berapa minimal jumlah sampel dapat dikatakan cukup?

Berdasarkan Central Limit Theorem (CLT) jumlah sampel sudah dikatakan cukup jika sudah mencapai 30 observasi.

3.2.4 Apakah hipotesis nol (H0) pasti merupakan dugaan/hipotesa negatif?

Tidak, tergantung kasus yang akan diuji. Hipotesis nol (H0) mengindikasikan keadaan awal atau kedaan yang tidak mengalami perubahan respon walaupun telah dilakukan suatu perlakuan.

3.2.5 Bagaimana cara melakukan tes/uji hipotesis ketika sampel data tidak berdistribusi normal?

Kita tetap dapat melakukan tes/uji hipotesis menggunakan tes/uji non-parametrik yang tidak mengharuskan sampel data berdistribusi normal, seperti Wilcoxon test untuk tes/uji hipotesis 1 sampel dan Mann-Whitney test untuk tes/uji hipotesis 2 sampel.

3.2.6 Jika ingin mengetahui pengaruh sistem kerja WFH terhadap kinerja karyawan menimbulkan efek positif/negatif/tidak ada efek, bagaiamana penentuan hipotesisnya?

• H0: Sistem kerja WFH tidak berpengaruh terhadap kinerja karyawan
• H1: Sistem kerja WFH berpengaruh terhadap kinerja karyawan (dapat berupa pengaruh positif ataupun negatif)

3.2.7 Perbedaan fungsi pnorm() dan qnorm()?

• Fungsi pnorm() digunakan untuk memperoleh nilai peluang ketika diketahui nilai z-score (z-score -> peluang). Sedangkan,
• fungsi qnorm() kebalikan dari fungsi pnorm(), digunakan untuk memperoleh nilai z-score ketika diketahui nilai peluang (peluang -> z-score)

3.2.8 Apa maksud dari pernyataan “Gagal tolak H0 != Terima H0 dan Tolak H0 != Terima H1”?

Ketika kita melakukan tes/uji hipotesis, hal yang kita peroleh sebenarnya adalah melihat bahwa data sampel yang dimiliki “menyimpang sangat ekstrem”. Sehingga, kita hendak mengambil kesimpulan bahwa sampel “dapat dikatakan signifikan”.

Pada tes/uji hipotesis, menolak H0 dapat dikatakan sebagai pemberian bukti sementara penerimaan H1. Secara absolut hanya dapat dilakukan ketika kita sudah mengecek data populasi , tetapi hal tersebut hampir tidak mungkin dilakukan. Sehingga, penggunaan bahasa yang tepat adalah “menolak H0” bukan bearti “menerima H1”

3.2.9 Berapa batasan nilai korelasi dikatakan kuat dan lemah?

Semakin mendekati 0, berarti korelasi cenderung lemah dan sebalikanya. Semakin mendekati 1, berarti korelasi cnderung kuat. Pada umumnya, jika nilai korelasi di bawah 0.5, berarti korelasi cenderung lemah dan sebaliknya. Jika nilai korelasi di atas 0.5, berarti korelasi cenderung kuat. Untuk mengetahui apakah nilai korelasi di bawah 0.5, sebenarnya berkorelasi lemah atau tidak berkorelasi dapat dipastikan dengan melakukan tes/uji statistik menggunakan fungsi cor.test()

3.2.10 Jika sampel data tidak berdistribusi normal, apakah z-score standarization dengan fungsi scale() masih tetap dapat digunakan?

Jika tujuannya hanya untuk melakukan scaling pada data (memperkecil interval pada data bertipe numerik) kita tetap dapat menggunakan z-score standarization walaupun sampel data tidak bersitribusi normal. Tetapi, ketika tujuannya adalah menghitung peluang, maka perhitungan z-score kurang tepat digunakan.

3.2.11 Jika nilai p-value yang diperoleh sama dengan nilai alpha yang digunakan, apakah kesimpulan yang dipilih tolak H0 atau gagal tolak H0?

Pada kasus nilai p-value sama dengan nilai alpha, secara aplikatif umumnya kesimpulan yang dipilih adalah tolak H0. Namun, ada baiknya menambah jumlah sampel untuk memperoleh dan memastikan kesimpulan yang diambil tidak menimbulkan kondisi yang ambigu.

3.2.12 Terdapat sumber yang mengatakan bahwa formula untuk menghitung z-score adalah $z=\frac{\overline{x}-{\mu }_0}{\frac{\sigma }{\sqrt{n}}}$, apakah formula tersebut benar?

Formula tersebut benar untuk menghitung z-score tes/uji hipotesis rata-rata 1 sampel.

3.2.13 Bagaimana cara melakukan tes/uji hipotesis untuk proporsi?

Fungsi yang digunakan masih sama seperti melakukan tes/uji hipotesis rata-rata, yaitu pnorm(), namun formula untuk menghitung z-score yang digunakan berbeda. Sehingga, harus dilakukan perhitungan z-score terlebih dahulu dengan formula

$$z=\frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}$$

Dengan $\text{p^}$ adalah proporsi sampel, $p0$ adalah proporsi populasi, dan $n$ adalah jumlah sampel yang diuji/dites. Selanjutnya nilai z-score tersebut yang di-input pada fungsi pnorm().

3.2.14 Mengapa jika tingkat alpha pada confidence interval semakin mendekati 0 (confidence interval 100%), selisih nilai batas bawah dan batas atas semakin besar?

Semakin kecil tingkat alpha, maka interval/selisih batas bawah dan batas atas pada confidence interval akan semakin besar, yang artinya rentang nilai prediksi semakin lebar. Secara sederhana, jika error yang ditoleransi mendekati 0%, maka nilai prediksi harus berada dalam interval/selisih batas bawah dan batas atas pada confidence interval. Supaya memenuhi syarat tersebut, maka interval harus dibuat semakin lebar untuk memastikan bahwa nilai prediksi berada di dalam interval tersebut.

3.2.15 Apakah taraf kepercayaan pada confidence interval selalu 95%?

Taraf kepercayaan 95% atau alpha 5% adalah taraf kepercayaan atau alpha yang sering digunakan oleh user. Taraf kepercayaan ataupun alpha yang digunakan sebenarnya boleh di angka berapa pun bergantung pada sudut pandan bisnis dan pemrasalahan yang dianalisis. Misal, untuk permasalahan di bidang kesehatan atau transportasi diharapkan error yang dihasilkan sekecil mungkin karena berkaitan dengan jiwa seseorang, maka biasanya digunakan taraf kepercayaan 99% atau alpha 1%.

Bab 4 Regression Model

4.1 Linear Regression

4.1.1 Bagaimana model regresi linier dengan fungsi lm() bekerja jika terdapat prediktor bertipe kategorik?

Fungsi lm() pada R akan secara otomatis mengubah prediktor bertipe kategorik menjadi variabel dummy. Variabel dummy adalah hasil transformasi prediktor kategorik berupa nilai 0 atau 1 untuk menggambarkan ada/tidaknya suatu kategori (metode untuk mengkuantitatifkan prediktor bertipe kategorik). Jika terdapat $k$ kategori pada suatu prediktor bertipe kategori, maka akan dihasilkan sejumlah $k-1$ variabel dummy. Misal, jika terdapat 1 kolom berisi prediktor bertipe kategorik yang menggambarkan tingkat salary dari setiap pelanggan sebagai berikut

#>   salary_level
#> 1         High
#> 2          Low
#> 3       Medium
#> 4          Low
#> 5         High

Maka, akan dihasilkan 2 variabel dummy seperti berikut

#>   salary_level_Low salary_level_Medium
#> 1                0                   0
#> 2                1                   0
#> 3                0                   1
#> 4                1                   0
#> 5                0                   0

4.1.2 Jika pada hasil summary model regresi linier terdapat salah satu level/kategori dari prediktor bertipe kategorik yang tidak signifikan mempengaruhi target variabel (p-value < alpha), apakah prediktor tersebut signifikan mempengaruhi target variabel atau tidak?

Keadaan tersebut biasanya disebabkan oleh jumlah sampel untuk level/kategori tersebut tidak cukup banyak dibandingkan dengan jumlah sampel level/kategori lainnya. Kesimpulan signifikan atau tidaknya kembali pada masing-masing user dengan mempertimbangkan sudut pandang bisnis dan permasalahan yang dianalisis. Namun, salah satu solusi yang dapat dicoba adalah menggabungkan sampel dengan level/kategori tersebut dengan level/kategori lainnya yang memiliki karakteristik yang serupa.

4.1.3 Fungsi lm() akan secara otomatis mengubah prediktor bertipe kategorik menjadi variabel dummy dimana level/kategori paling awal akan dijadikan sebagai basis (dihilangkan). Apakah hasil analisis model regresi linier akan berubah, jika dilakukan pengurutan ulang (reorder) level/kategori dari suatu prediktor bertipe kategorik?

Hasil analisis model regresi linier yang diperoleh tidak akan berubah, melakukan pengurutan ulang level/kategori dari suatu prediktor numerik hanya akan mengubah basis yang digunakan.

4.1.4 Jika pada hasil summary model regresi linier terdapat prediktor yang tidak signifikan, apakah prediktor tersebut lebih baik tidak diikutsertakan dalam model regresi linier atau sebaliknya?

Hal tersebut bergantung pada sudut pandang bisnis dan permasalahan yang dianalisis, jika berdasarkan sudut pandang bisnis prediktor tersebut harus diketahui bagaimana dan seberapa besar pengaruhnya terhadapap target variabel. Maka, tetap dapat diikutsertakan. Namun, jika berdasarkan sudut pandang bisnis tidak terlalu mempengaruhi target variabel, maka boleh tidak diikutsertakan dengan tujuan supaya model regresi linier yang dihasilkan menjadi lebih sederhana. Solusi lain yang dapat dipertimbangkan untuk dilakukan adalah menambah jumlah sampel atau membuang observasi yang merupakan outlier dan berpengaruh negatif terhadap hasil analisisi regresi linier. Hal ini dapat dipertimbangkan untuk dilakukan karena suatu prediktor tidak signifikan mempengaruhi target tidak hanya karena antara prediktor dengan target tidak saling mempengaruhi dan dipengaruhi, melainkan juga karena beberapa faktor seperti variansi data yang rendah atau karena terdapat observasi outlier yang justru berpengaruh negatif terhaddap hasil analisis regresi linier.

4.1.5 Apa saja cara yang dapat dilakukan untuk memperbaiki model regresi linier (tuning)?

Berikut beberapa cara yang dapat dilakukan untuk memperbaiki model regresi linier:

1. Deteksi observasi outlier
   • Pengaruh negatif terhadap model regresi linier sebaiknya observasi tersebut tidak diikutsertakan
   • Pengaruh positif terhadap model regresi linier sebaiknya observasi tersebut tetap dapat diikutsertakan
2. Menambah prediktor berdasarkan informasi dari prediktor yang sudah ada (feature engineering)
3. Melakukan transformasi data
   • Mengubah prediktor bertipe numerik menjadi kategorik
   • Melakukan transformasi pada prediktor bertipe numerik dengan operasi matematika seperti log, ln, sqrt, kuadrat, dll

4.1.6 Apa kegunaan nilai p-value pada hasil summary model regresi linier, padahal biasanya dilakukan pemeriksaan nilai korelasi atau tes/uji korelasi sebelum melakukan pemodelan regresi linier?

Memeriksa nilai korelasi atau melakukan tes/uji korelasi bertujuan untuk melihat keterkaitan antara prediktor dengan target variabel, dimana secara logika (hipotesis) variabel yang saling berkaitan ada kemungkinan untuk saling mempengaruhi dan dipengaruhi. Sementara, nilai p-value pada hasil summary model regresi linier digunakan untuk mengkonfirmasi apakah antara prediktor dan target saling mempengaruhi dan dipengaruhi. Sebab, korelasi hanya menyatakan keterkaitan antar variabel saja, bukan menjelaskan hubungan sebab dan akibat.

4.1.6.1 Apakah regresi linier dapat dilakukan jika target variabel bertipe numerik diskrit?

Bisa saja, namun hasil prediksinya kurang tepat karena menghasilkan nilai numerik kontinu yang kemungkinan menghasilkan error yang lebih besar. Model regresi yang lebih cocok digunakan untuk kondisi tersebut adalah model regresi poisson, untuk penjelasan lengkapnya dapat membaca link referensi berikut Regresi Poisson

4.1.7 Apakah cukup dengan mengecek nilai korelasi atau harus dilakukan tes/uji korelasi untuk mengecek keterkaitan antara prediktor dengan target variabel?

Nilai korelasi di bawah -0.5 atau di atas 0.5 sudah dianggap bahwa antara prediktor dan target variabel memiliki keterkaitan/hubungan yang cukup kuat. Namun, sebaliknya nilai korelasi di antara -0.5 sampai 0.5 mengindikasikan bahwa antara prediktor dengan target saling berkaitan/berhubungan, tetapi hubungannya lemah. Sehingga, perlu dilakukan tes/uji korelasi untuk mengonfirmasi apakah hubungan antara prediktor dengan target variabel signifikan atau tidak secara statistik (objektif).

4.1.8 Hasil summary model regresi linier dari fungsi lm() memuat beberapa nilai seperti std.error, t-value, dan p-value. Apa kegunaan dari ketiga nilai tersebut?

Std.error dan t-value pada hasil summary model regresi linier digunakan untuk menghitung nilai p-value. Dimana nilai p-value digunakan untuk melakukan tes/uji hipotesis untuk menguji apakah prediktor signifikan mempengaruhi target variabel atau tidak. Hipotesis:

• H0: Prediktor tidak mempengaruhi target variabel
• H1: Prediktor mempengaruhi target variabel

Nilai p-value tersebut harus dibandingkan dengan alpha yang digunakan (p-value < alpha: prediktor signifikan mempengaruhi target variabel) untuk menarik kesimpulan apakah prediktor signifikan mempengaruhi target atau tidak. Namun, hasil summary model regresi linier di R sudah dilengkapi oleh simbol bintang yang mempermudah user untuk menarik kesimpulan. Jika minimal terdapat satu simbol bintang, maka prediktor signifikan mempengaruhi target variabel dengan alpha 5% (p-value < 0.05).

4.1.9 Bagaimana cara menampilkan nilai p-value pada output linear model (regresi linier)?

Output dari fungsi lm() di R dapat dilihat melalui fungsi summary(). Output tersebut berupa list yang dapat diakses sesuai dengan aturan indexing dan subsetting pada list.

lm_mtcars <- lm(mpg ~ cyl, mtcars)
summary(lm_mtcars)

#> 
#> Call:
#> lm(formula = mpg ~ cyl, data = mtcars)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -4.9814 -2.1185  0.2217  1.0717  7.5186 
#> 
#> Coefficients:
#>             Estimate Std. Error t value             Pr(>|t|)    
#> (Intercept)  37.8846     2.0738   18.27 < 0.0000000000000002 ***
#> cyl          -2.8758     0.3224   -8.92       0.000000000611 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 3.206 on 30 degrees of freedom
#> Multiple R-squared:  0.7262,	Adjusted R-squared:  0.7171 
#> F-statistic: 79.56 on 1 and 30 DF,  p-value: 0.0000000006113

Untuk mengambil nilai pada index coefficient, dapat menggunakan fungsi summary(model)$coefficient yang akan menghasilkan output berupa matrix

summary(lm_mtcars)$coefficient

#>             Estimate Std. Error   t value                   Pr(>|t|)
#> (Intercept) 37.88458  2.0738436 18.267808 0.000000000000000008369155
#> cyl         -2.87579  0.3224089 -8.919699 0.000000000611268714258098

Kemudian untuk mengambil p-value dari matrix di atas dapat menggunakan aturan indexing dan subsetting pada matrix, dimana nilai yang ingin diambil berada pada kolom ke-4

summary(lm_mtcars)$coefficient[, 4]

#>                (Intercept)                        cyl 
#> 0.000000000000000008369155 0.000000000611268714258098

4.2 Evaluation

4.2.1 Apakah nilai AIC bisa negatif?

AIC dapat bernilai negatif atupun positif bergatung pada nilai maksimum likelihood yang diperoleh. Berikut formula untuk menghitung nilai AIC:

$$AIC=2k-2l{n}_L$$

Dimana $k$ merupakan jumlah parameter yang diprediksi (prediktor dan intersep) dan $L% merupakan nilai maksimum likelihood yang diperoleh.

Namun, pemilihan model regresi linier pada metode stepwise regression tidak memperhatikan tanda negatif atau positif dari nilai AIC melainkan nilainya saja (absolut AIC). Sehingga, tanda negatif atau positif pada nilai AIC tidak berpengaruh dalam proses pemilihan model regresi linier pada metode stepwise regression. Model yang dipilih adalah model yang memiliki nilai abolut AIC terkecil yang mengindikasikan bahwa semakin sedikit informasi yang hilang pada model tersebut. Negative values for AIC

4.2.2 Apa perbedaan R-squared dan Adjusted R-squared?

• R-Squared: Seberapa baik model menjelaskan data, dengan mengukur seberapa besar informasi (variansi) dari target dapat dijelaskan oleh prediktor. Sehingga, jelas ketika prediktor bertmabah, informasi (variansi) yang dirangkum semakin banyak atau dengan kata lain jelas nilai R-Squared akan meningkat.
• Adj. R- Squared: tidak demikian pada adj. r-squared, karena disesuaikan dengan jumlah prediktor yang digunakan. Adj. r-squared akan meningkat hanya jika prediktor baru yang ditambahkan mengarah pada hasil prediksi yang lebih baik (prediktor signifikan mempengaruhi target)

Formula Adj. R-Squared:

$$R_{adj}^2=1-(1-R^2)\frac{n-1}{n-p-1}$$

Dimana, $n$ adalah jumlah sampel dan $p$ adalah jumlah prediktor.

4.2.3 Adakah batasan nilai R-squared yang dianggap baik?

Baik tidaknya nilai R-squared adalah relatif bergantung pada sudut pandang bisnis dan permasalahan yang dianalisis. Namun, umumnya nilai R-squared di atas atau sama dengan 70% sudah cukup baik dalam menjelaskan variansi dari target variabel.

4.2.4 Apakah hanya nilai AIC yang dapat digunakan untuk memilih model regresi linier pada stepwise regression?

Secara default fungsi stepwise() di R hanya menngunakan nilai AIC untuk memilih model regresi linier. Jika ingin membandingkan metrics evaluasi lain dapat menggunakan fungsi compare_performance() dari package performance untuk menampilkan beberapa nilai metrics evaluasi seperti R-squared, BIC, dll untuk setiap kombinasi model yang dibuat. Berikut beberapa alasan mengapa nilai AIC lebih diutmakan untuk memilih model regresi linier dibandingkan metrics lainnya Alasan Penggunaan nilai AIC

4.2.5 Stepwise regression memiliki 3 algoritma, yaitu backward, forward, dan both. Apakah ketiga algoritma tersebut memiliki fungsi yang sama?

Stepwise regression baik algoritma backward, forward, ataupun both memiliki fungsi yang sama, yaitu untuk melakukan pemilihan prediktor (variable selection) yang akan diikutsertakan dalam model regresi linier. Stepwise regession baik dengan algoritma backward, forward, ataupun both akan menghasilkan performa model yang hampir sama, namun ada baiknya sebagai user melakukan trial and error dari ketiga algoritma tersebut. Kemudian, memilih model regresi linier yang memiliki R-squared adjusted tertinggi dan nilai AIC paling kecil.

4.2.6 Adakah batasan nilai AIC yang dianggap kecil?

Nilai AIC memiliki interval dari -inf sampai +inf, sehingga tidak ada ketentuan yang menyatakan berapa nilai AIC yang dianggap kecil. Namun, untuk mengetahui apakah kombinasi model regresi linier yang dihasilkan sudah baik atau belum, user dapat melihat penurunan/peningkatan nilai AIC. Jika ketika melakukan stepwise regression baik dengan metode forward, backward, ataupun both nilai AIC sudah tidak mengalami penurunan, justru mengalami kenaikan ketika ditambah/dikurangkan prediktornya, maka iterasi sudah berhenti pada kombinasi model sebelum terjadi peningkatan nilai AIC.

4.3 Assumption

4.3.1 Mengapa pada asumsi normality yang harus berdistribusi normal adalah error/residual?

Nilai error/residual yang diharapkan untuk setiap analisis termasuk regrsi linier adalah 0, untuk memastikan bahwa hasil prediksi untuk setiap observasi mendekati atau sama dengan 0, maka diharapkan error/residual berdistribusi normal dimana nilai rata-rata error/residual sama dengan 0. Error/residual pada regresi linier seringkali tidak berdistribusi normal disebabkan oleh beberap faktor, yaitu:

• Model yang digunakan tidak cocok, misal hubungan antara prediktor dengan target variabel tidak linier melainkan kudratik/eksponensial/dll
• Terdapat observasi outlier

4.3.2 Mengapa perlu dilakukan pengecekkan asumsi model regresi linier?

Supaya interpretasi dan hasil prediksi dari model regresi linier bersifat BLUE (Best, Linear, Unbiased Estimator). Secara sederhana, hasil analisis regresi linier dapat berlaku secara objektif dan konsisten.

4.3.3 Jika sudah mencoba berbagai solusi untuk memperbaiki model regresi linier supaya asumsi terpenuhi, tetapi masih terdapat asumsi yang tidak terpenuhi apa yang harus dilakukan?

Hal tersebut berarti kondisi data historis yang tersedia tidak cocok dianalisis menggunakan model regresi linear. Anda dapat mencoba menganalisis data tersebut menggunakan metode/model lainnya seperti tree based method (regression tree) yang juga dapat dinterpretasikan dan free assumption.

4.3.4 Bagaiamna cara melakukan tes/uji normality terhadap error/residual jika jumlah sampel yang digunakan lebih dari 5000?

Anda dapat melakukan tes/uji normality terhadap error/residual menggunakan uji Kolmogorov Smirnov. Berikut contoh cara melakukan uji Kolmogorov Smirnov di R:

ks.test(model$residuals, "pnorm", mean = mean(model$residuals), sd = sd(model$residuals))

4.3.5 Bagaimana cara melakukan tes/uji korelasi antara prediktor dengan target variabel secara langsung untuk semua prediktor di R?

Fungsi yang digunakan untuk melakukan tes/uji korelasi di R adalah cor.test() sebagai berikut:

copiers <- read.csv("data/03-RM/copiers.csv") %>% select(-Row.ID)
cor.test(copiers$Sales, copiers$Profit)

#> 
#> 	Pearson's product-moment correlation
#> 
#> data:  copiers$Sales and copiers$Profit
#> t = 21.26, df = 60, p-value < 0.00000000000000022
#> alternative hypothesis: true correlation is not equal to 0
#> 95 percent confidence interval:
#>  0.9013320 0.9632858
#> sample estimates:
#>       cor 
#> 0.9395785

Dengan hipotesis

• H0: Prediktor dan target tidak saling berkorelasi
• H1: Prediktor dan target saling berkorelasi

Anda dapat membuat suatu fungsi yang mengaplikasikan fungsi cor.test() di atas untuk setiap prediktor sebagai berikut:

cor.test.all <- function(data,target) {
  names <- names(data %>% select_if(is.numeric))
  df <- NULL
  for (i in 1:length(names)) {
    y <- target
    x <- names[[i]] 
    p_value <- cor.test(data[,y], data[,x])[3]
    temp <- data.frame(x = x,
                       y = y,
                       p_value = as.numeric(p_value))
    df  <- rbind(df,temp)
  }
  return(df)
}

cor.test.all(data = copiers, target ="Profit")

#>          x      y                               p_value
#> 1    Sales Profit 0.00000000000000000000000000001271056
#> 2 Quantity Profit 0.00000000076036803959617475451651658
#> 3 Discount Profit 0.00044956416337473974241881191638015
#> 4   Profit Profit 0.00000000000000000000000000000000000

4.3.6 Apa akibat jika asumsi no-multicolinearity tidak terpenuhi?

Model regresi linier yang dihasilkan menjadi tidak efisien karena terdapat informasi yang redundan (sama). Ada baiknya model regresi linier yang dipilih adalah model regresi linier yang paling efisien dan sederhana dengan performa yang cukup baik (error yang dihasilkan relatif kecil)

4.4 Mathematics Formula

Untuk mengestimasi nilai koefisien (beta), pertama-tama coba ingat kembali beberapa konsep pada workshop “Practical Statistics”. Variance merupakan nilai yang menggambarkan seberapa bervariasi/beragamnya suatu variabel bertipe numerik/angka. Semakin besar nilai variance maka semakin beragam nilai dalam satu variabel (heterogen), sedangkan semakin kecil nilai variance maka semakin sama/mirip setiap observasi pada satu variabel (homogen). Data yang observasinya bernilai sama, maka variance sama dengan 0.

Sementara covariance merupakan nilai yang menggambarkan hubungan (positif/negatif/tidak ada hubungan) antara dua variabel numerik. Namun covariance tidak dapat menggambarkan seberapa erat/kuat hubungan tersebut karena nilai covariance tidak memilki batasan yang mutlak (- inf, + inf).

Dalam notasi matematika, anggap kita memiliki data yang terdiri dari 2 variabel, yaitu, $(X_i,Y_i)$, maka secara empiris nlai covariance diperoleh dari:

$$Cov(X,Y)=\frac{1}{n-1}\sum _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})$$

bisa juga diperoleh dari,

$$Cov(X,Y)=\frac{1}{n-1}(\sum _{i=1}^n{X}_i{Y}_i-n\overline{X}\overline{Y})$$

Jika formula dari covariance cukup rumit, coba ingat kembali formula dari variance:

$$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\overline{X}{)}^2$$

pahami bahwa perbedaan variance dan covariance adalah variance hanya mengacu pada 1 variabel, sedangkan covariance mengacu pada 2 variabel. Maka, formula dari covariance:

$$Cov(X,Y)=\frac{1}{n-1}\sum _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})$$

Seperti yang telah dijelaskan di atas bahwa covariance menjelaskan jenis hubungan antara 2 variabel numerik. Namun, kita tidak dapat menilai seberapa erat/kuat hubungan antara keduanya karena interval nilai covariance yang tidak memiliki batasan. Oleh karena itu, kita bisa melakukan standarization terlebih dahulu terhadap 2 variabel numerik tersebut yang mengacu pada definisi correlation:

$$Cor(X,Y)=\frac{Cov(X,Y)}{S_x{S}_y}$$

beberapa fakta mengenai correlation:

• Cor(X,Y) = Cor(Y,X)
  
• -1 <= Cor(X,Y) <= 1
  
• Nilai correlation mendekati 1 artinya kedua variabel berhubungan erat dan hubungannya linier positif
  
• Nilai correlation mendekati -1 artinya kedua variabel berhubungan erat dan hubungannya linier negatif
• Nilai correlation mendekati 0 artinya kedua variabel tidak saling berhubungan secara linier

Untuk menggambarkan persebaran observasi antara x dan y, dapat dilakukan dengan menarik suatu garis lurus yang menggambarkan keseluruhan persebaran data. Dimana, untuk menarik suatu garis lurus diperlukan titik awal ($b0$) dan kemiringan garis ($b1$).

Lalu bagaimana cara mengestimasi $b0$ dan $b1$ yang optimal (dimana garis linier dapat menggambarkan keseluruhan persebaran data). Kita bisa menggunakan konsep kuadrat terkecil, untuk menemukan kombinasi $b0$ dan $b1$ yang meminimumkan jarak kuadrat antara titik pengamatan dengan garis linier:

$$\sum _{i=1}^n\{Y_i-({\beta }_0+{\beta }_1{X}_i){\}}^2$$

• Estimasi slope:

$${\hat{\beta }}_1=Cor(Y,X)\frac{Sd\left(Y\right)}{Sd\left(X\right)}$$

• Estimasi intercept:

$${\hat{\beta }}_0=\overline{Y}-{\hat{\beta }}_1\overline{X}$$

R-square secara definisi adalah persentase total keragaman suatu target variabel yang dapat dijelaskan oleh prediktor variabel (model), dengan formula:

$$R^2=1-\frac{\sum _{i=1}^n(\widehat{Y_i}-\overline{Y}{)}^2}{\sum _{i=1}^n(Y_i-\overline{Y}{)}^2}$$

Beberapa fakta tentang R-square ($R^2$):

• $R^2$ adalah persentase total keragaman suatu target variabel yang dapat dijelaskan oleh model regresi
  
• $0\le R^2\le 1$

Namun, penggunaan R-square seringkali keliru karena adanya batasan dalam penggunaan metrik ini. R-square cenderung meningkat setiap penambahan variabel prediktor, walaupun variabel prediktor tersebut tidak mempengaruhi variabel target secara signifikan. Akibatnya, model dengan variabel prediktor yang lebih banyak mungkin tampak lebih baik hanya karena memiliki lebih banyak variabel prediktor saja.

Berbeda dengan Adjusted R-square yang tidak mengalami peningkatan setiap penambahan variabel prediktor karena adjusted R-square meningkat hanya ketika variabel prediktor baru benar-benar mengarah ke prediksi yang lebih baik (signifikan mempengaruhi variabel target).

Formula adjusted R-squared:

$$R_{adj}^2=1-(1-R^2)\frac{n-1}{n-p-1}$$

Dimana $n$ adalah jumlah pengamatan dan $p$ adalah jumlah prediktor. Perhatikan bahwa ketika $p$ meningkat, $\frac{n-1}{n-p-1}$ akan mengecil dan mendorong nilai adjusted R-square secara keseluruhan menjadi kecil.

Salah satu alat statistik yang dapat digunakan untuk mengecek ada/tidak multicolinearity adalah Variance Inflation Factor (VIF). VIF mengukur peningkatan estimasi koefisien beta, jika antar prediktor saling berkorelasi. Secara matematis, nilai VIF diperoleh dengan meregresikan setiap prediktor dengan prediktor lain. Contoh: diketahui terdapat $X1,X2,...,Xn$, nilai VIF untuk $X1$ diperoleh dari hasil regresi $X1$ dengan $X2,...,Xn$, dst. Hasil regresi tersebut kemudian diterapkan pada formula berikut:

$$VIF=\frac{1}{1-R^2\left(x\right)}$$

Secara umum jika nilai VIF yang diperoleh lebih besar atau sama dengan 10, mengindikasikan terjadi multicolinearity (antar prediktor saling berkorelasi kuat).

Bab 5 Classification 1

5.1 Classification in General

5.1.1 Pada kasus klasifikasi, penentuan kelas didasarkan pada peluang. Bagaimana jika peluang yang diperoleh sama besar, misalnya pada kasus klasifikasi biner diperoleh peluang masuk ke kelas positif adalah 0.5 dan peluang masuk ke kelas negatif juga 0.5?

Hal tersebut bergantung pada user yang menentukan threshold/batasan probability untuk masuk ke kelas positif atau masuk ke kelas negatif. Namun, pada umumnya jika diperoleh probability $>=0.5$ maka observasi tersebut akan masuk ke kelas positif.

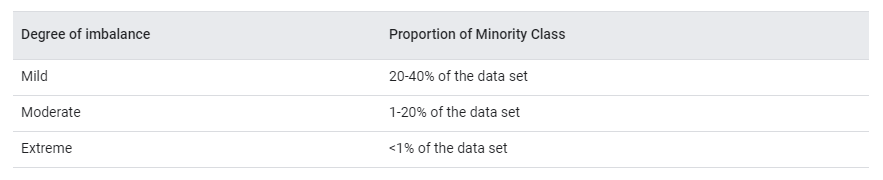
5.1.2 Permasalahan apa yang paling sering ditemui pada kasus klasifikasi?

Permasalahan yang sering ditemui pada kasus klasifikasi adalah proporsi target variabel yang tidak seimbang. Pada data di lapangan, nyatanya jumlah kelas positif jauh lebih sedikit dibandingkan kelas negatif. Contohnya:

• Perbankan: fraud detection, loan default
• Penerbangan: delay prediction
• Digital marketing: customer churn
• Kesehatan: cancer detection
• HR: employee attrition
• dan masih banyak lagi

Misalkan pada kasus fraud detection, dari 1000 transaksi yang terjadi, hanya 10 diantaranya fraud. Hal tersebut akan berpengaruh terhadap kemampuan model untuk memprediksi target, karena model klasifikasi sangat bergantung pada jumlah setiap level target dalam proses learning-nya. Model klasifikasi cenderung lebih pintar dalam memprediksi kelas mayoritas. Hal ini menjadi masalah yang cukup serius, sehingga perlu dilakukan penanganan lebih lanjut.

attrition <- read_csv("data/04-C1/attrition.csv") %>% 
  mutate(attrition = as.factor(attrition))

prop.table(table(attrition$attrition)) %>% round(2)

#> 
#>   no  yes 
#> 0.84 0.16

Salah satu cara yang paling umum untuk menyeimbangkan proporsi target variabel adalah dengan metode sampling, yaitu downsampling dan upsampling.

• Downsampling adalah proses sampling pada observasi kelas mayoritas sebanyak jumlah observasi pada kelas minoritas. Proses downsampling akan mengurangi jumlah observasi pada kelas mayoritas, sehingga memungkinkan terjadinya kehilangan informasi.

• Upsampling adalah proses sampling pada observasi kelas minoritas sebanyak jumlah observasi pada kelas mayoritas. Proses upsampling akan menambah jumlah observasi pada kelas minoritas, sehingga hanya menduplikasi data yang terdapat pada kelas minoritas.

Berikut contoh downsampling dan upsampling dengan menggunakan fungsi pada library caret dan recipes:

Sebelum menerapkan downsampling dan upsampling terlebih dahulu dilakukan cross validation, yaitu membagi data menjadi training set untuk proses pemodelan dan testing set untuk melakukan evaluasi. Cross validation dilakukan dengan menggunakan fungsi initial_split() dari library rsample. Fungsi tersebut akan melakukan proses sampling dengan metode stratified random sampling, sehingga proporsi target variabel pada data awal dipertahankan dengan baik pada training set maupun testing set.

# define seed
set.seed(100)

# menentukan indeks untuk train dan test
splitted <- initial_split(data = attrition,
                          prop = 0.75,
                          strata = "attrition")

# mengambil indeks data train
train <- training(splitted)

# mengambil indeks data test`
test <- testing(splitted)

# proporsi data train
prop.table(table(train$attrition)) %>% round(2)

#> 
#>   no  yes 
#> 0.84 0.16

# proporsi data test
prop.table(table(test$attrition)) %>% round(2)

#> 
#>   no  yes 
#> 0.84 0.16

Downsampling dan upsampling hanya dilakukan pada data train karena proses pembuatan model klasifikasi hanya dilakukan pada data train. Data test dianggap sebagai unseen data yang hanya digunakan untuk mengevaluasi model.

• Cara downsampling menggunakan downSample() dari library caret

train_down <- downSample(x = train[, -1],
                         y = train$attrition,
                         yname = "attrition")

prop.table(table(train_down$attrition)) %>% round(2)

#> 
#>  no yes 
#> 0.5 0.5

• Cara upsampling menggunakan upSample() dari library caret

train_up <- upSample(x = train[, -1],
                     y = train$attrition,
                     yname = "attrition")

prop.table(table(train_up$attrition)) %>% round(2)

#> 
#>  no yes 
#> 0.5 0.5

Berikut dokumentasi official dari library caret: downSample: Down- and Up-Sampling Imbalanced Data

• Cara downsampling/upsampling dengan recipes

Seperti saat menggunakan fungsi pada library caret, ketika menggunakan fungsi dari library recipes juga harus dilakukan cross validation terlebih dahulu. Perbedaan ketika menggunakan fungsi dari library recipes adalah data train dan test tidak di-assign ke dalam sebuah objek melainkan dilakukan downsampling atau upsampling terlebih dahulu.

set.seed(417)

splitted_rec <- initial_split(data = attrition,
                              prop = 0.8,
                              strata = "attrition")

splitted_rec

#> <Analysis/Assess/Total>
#> <1177/293/1470>

Gunakan fungsi step_downsample() atau step_upsample() yang didefinisikan dalam sebuah recipe.

rec <- recipe(attrition ~ ., training(splitted)) %>% 
  
  # `step_downsample()` dapat diganti dengan `step_upsample()`
  step_downsample(attrition, ratio = 1, seed = 100) %>%
  
  prep()

# membuat data train dengan fungsi `juice()`
train_rec <- juice(rec)

# membuat data test dengan fungsi `bake()`
test_rec <- bake(rec, testing(splitted))

prop.table(table(train_rec$attrition)) %>% round(2)

#> 
#>  no yes 
#> 0.5 0.5

Berikut dokumentasi official dari library recipes: tidymodels/recipes

5.2 Logistic Regression

5.2.1 Bagaimana model logistic regression menggunakan variabel kategorik sebagai prediktor?

Sama seperti kasus linear regression, pada logistic regression variabel kategorik harus diubah menjadi dummy variabel. Pada fungsi glm() sudah otomatis melakukan transformasi dummy variabel untuk kolom yang bertipe data character atau factor.

5.2.2 Bagaimana jika terdapat salah satu level pada prediktor kategorik yang tidak signifikan (p-value > alpha)? Apakah prediktor tersebut masih dianggap signifikan mempengaruhi target?

Level yang menjadi basis akan dianggap signifikan, sedangkan untuk level lainnya yang tidak signifikan artinya level tersebut tidak memberikan pengaruh terhadap target variabel. Solusi yang dapat dilakukan adalah:

• Binning, yaitu level tersebut digabungkan dengan level lainnya yang mirip dan signifikan
• Menambahkan jumlah observasi pada level yang tidak signifikan tersebut.

5.2.3 Pada fungsi lm() sudah otomatis melakukan transformasi data kategorik dengan level pertama yang dijadikan basis. Apakah pengubahan urutan level (reorder) akan mengubah hasil pemodelan?

Nilai p-value pada setiap level tidak akan berubah ketika kita melakukan reorder level. Interpretasi untuk variabel kategorik bergantung pada level yang dijadikan basis.

5.2.4 Apa pengertian dari Null Deviance dan Residual Deviance pada summary model?

• Null deviance menunjukkan seberapa baik model memprediksi target variabel hanya berdasarkan nilai intercept, tidak menggunakan predictor apapun.
• Residual deviance menunjukkan seberapa baik model memprediksi target variabel berdasarkan nilai intercept dan semua prediktor yang digunakan dalam model. Umumnya nilai Residual deviance lebih kecil dibandingkan null deviance.

Note: Null dan residual deviance hanya sebagian kecil tools yang bisa kita gunakan untuk mengevaluasi model mana yang paling baik. Namun perlu dijadikan catatan bahwa semakin banyak prediktor yang digunakan, nilai residual deviance pasti lebih kecil sehingga evaluasi menjadi bias. Pada praktiknya, confusion matrix lebih sering digunakan untuk melakukan evaluasi model klasifikasi.

Berikut link eksternal yang dapat dijadikan sebagai bahan referensi: Null deviance & Residual deviance

5.2.5 Apa itu Fisher Scoring pada summary model?

Fisher scoring adalah turunan dari metode Newton untuk mengatasi Maximum Likelihood. Fisher scoring memberikan informasi berapa banyak iterasi yang dilakukan pada model sehingga diperoleh nilai parameter pada summary.

5.2.6 Apa itu Maximum Likelihood Estimator (MLE)?

Nilai estimate pada model logistic regression diperoleh dengan pendekatan MLE. MLE merupakan pendekatan statistik untuk mendapatkan nilai estimate yang optimum pada model.

5.2.7 Apa yang dimaksud dari nilai Akaike Information Criterion (AIC)?

AIC menggambarkan seberapa banyak informasi yang hilang pada model tersebut. Nilai AIC sendiri tidak dapat diinterpretasi, berbeda dengan R-squared, karena tidak memiliki range tertentu. Sehingga Nilai AIC digunakan untuk membandingkan kualitas dari beberapa model. Semakin kecil nilai AIC, semakin sedikit informasi yang hilang, yang artinya semakin baik model kita dalam menangkap pola data.

5.2.8 Bagaimana cara untuk mengindikasi adanya perfect separation pada model?

• Tidak ada prediktor yang signifikan padahal nilai AIC sangat kecil
  
• Terdapat 1 nilai estimate yang nilainya cukup besar dibandingkan yang lain
  
• Gunakan parameter method = "detect_separation" untuk mendeteksi adanya perfect separation pada model:

honors <- read.csv("data/04-C1/sample.csv")

library(brglm2)
glm(hon ~ female + read + math + write,
    data = honors,
    family = "binomial",
    method = "detect_separation")

#> Separation: TRUE 
#> Existence of maximum likelihood estimates
#> (Intercept)      female        read        math       write 
#>        -Inf        -Inf        -Inf        -Inf         Inf 
#> 0: finite value, Inf: infinity, -Inf: -infinity

Output Separation: TRUE menandakan adanya perfect separation pada model. Untuk mengetahui variabel mana yang merupakan perfect separation, kita perlu amati output dari summary() model.

5.2.9 Bagaimana Logistic Regression untuk kasus multiclass classification?

Multiclass classification adalah kasus klasifikasi dengan lebih dari 2 levels pada target variable. Contohnya pada data iris kita ingin mengklasifikasi apakah sebuah bunga termasuk kelas setosa, versicolor, atau virginica.

levels(iris$Species)

#> [1] "setosa"     "versicolor" "virginica"

Lakukan train-test splitting dengan proporsi 80-20 persen.

set.seed(100)
idx <- sample(nrow(iris), 0.8*nrow(iris))
iris_train <- iris[idx,]
iris_test <- iris[-idx,]

Pembuatan model multiclass classification dapat menggunakan fungsi multinom() dari library nnet, dengan menyertakan parameter formula dan data.

library(nnet)
iris_multi <- multinom(formula = Species ~ ., data = iris_train)

#> # weights:  18 (10 variable)
#> initial  value 131.833475 
#> iter  10 value 12.613035
#> iter  20 value 1.598061
#> iter  30 value 0.583494
#> iter  40 value 0.373022
#> iter  50 value 0.306030
#> iter  60 value 0.267677
#> iter  70 value 0.236148
#> iter  80 value 0.196360
#> iter  90 value 0.125961
#> iter 100 value 0.120334
#> final  value 0.120334 
#> stopped after 100 iterations

summary(iris_multi)

#> Call:
#> multinom(formula = Species ~ ., data = iris_train)
#> 
#> Coefficients:
#>            (Intercept) Sepal.Length Sepal.Width Petal.Length Petal.Width
#> versicolor    30.78627    -9.027769   -6.721883     16.02937   -8.216299
#> virginica    -52.10505   -45.676726  -55.277893     88.90439   48.300727
#> 
#> Std. Errors:
#>            (Intercept) Sepal.Length Sepal.Width Petal.Length Petal.Width
#> versicolor    475.4254     102.3678    105.1483     182.5314    297.8557
#> virginica     945.3978     173.0019    138.9215     376.6561    420.8273
#> 
#> Residual Deviance: 0.2406676 
#> AIC: 20.24067

Dari model summary di atas, kita dapat menuliskan formula logistic regression sebagai berikut:

$$log-odds\left(versicolor\right)=30.78627-9.027769Sepal.Length-6.721883Sepal.Width+16.02937Petal.Length-8.216299Petal.Width$$

$$log-odds\left(virginica\right)=-52.10505-45.676726Sepal.Length-55.277893Sepal.Width+88.90439Petal.Length+48.300727Petal.Width$$

dengan $$Prob\left(setosa\right)=1-Prob\left(versicolor\right)-Prob\left(virginica\right)$$

Gunakan fungsi predict() dengan parameter type = "probs" untuk mengembalikan nilai probabilitas untuk masing-masing kelas.

iris_pred_prob <- predict(iris_multi,
                          newdata = iris_test,
                          type = "probs")

data.frame(iris_pred_prob) %>% round(8)

#>         setosa versicolor virginica
#> 1   0.99999998 0.00000002 0.0000000
#> 6   1.00000000 0.00000000 0.0000000
#> 10  0.99998435 0.00001565 0.0000000
#> 11  1.00000000 0.00000000 0.0000000
#> 13  0.99998478 0.00001522 0.0000000
#> 21  0.99999975 0.00000025 0.0000000
#> 33  1.00000000 0.00000000 0.0000000
#> 34  1.00000000 0.00000000 0.0000000
#> 38  0.99999989 0.00000011 0.0000000
#> 39  0.99995016 0.00004984 0.0000000
#> 50  0.99999985 0.00000015 0.0000000
#> 64  0.00000000 1.00000000 0.0000000
#> 67  0.00000000 1.00000000 0.0000000
#> 72  0.00003258 0.99996742 0.0000000
#> 73  0.00000000 0.00123755 0.9987624
#> 74  0.00000000 1.00000000 0.0000000
#> 76  0.00004259 0.99995741 0.0000000
#> 77  0.00000011 0.99999989 0.0000000
#> 79  0.00000004 0.99999996 0.0000000
#> 84  0.00000000 0.00000000 1.0000000
#> 90  0.00000002 0.99999998 0.0000000
#> 101 0.00000000 0.00000000 1.0000000
#> 103 0.00000000 0.00000000 1.0000000
#> 106 0.00000000 0.00000000 1.0000000
#> 108 0.00000000 0.00000000 1.0000000
#> 109 0.00000000 0.00000000 1.0000000
#> 117 0.00000000 0.00000000 1.0000000
#> 131 0.00000000 0.00000000 1.0000000
#> 134 0.00000000 0.00122746 0.9987725
#> 145 0.00000000 0.00000000 1.0000000

5.2.10 Mengapa fungsi glm() menghitung log of odds pada saat proses training model regresi logistik?

Secara sederhana fungsi log yang diterapkan pada nilai odds berguna untuk membuat jarak semula (0) sama untuk kedua peluang, yaitu peluang kelas 0 dan peluang kelas 1. Untuk lebih detailnya Anda dapat membaca referensi berikut WHAT and WHY of Log Odds

5.3 K-Neaest Neighbor

5.3.1 Bagaimana cara menghitung jarak eucledian dari multiple prediktor (lebih dari 2 prediktor)?

Tetap dilakukan menggunakan penghitungan eucledian distance, misal menghitung jarak euclidian dari prediktor (a, b, dan c)

$$e^2=a^2+b^2+c^2$$

Untuk lebih detailnya Anda dapat membaca referensi berikut Euclidean Distance In ‘n’-Dimensional Space

5.4 Model Evaluation

5.4.1 Apa yang dimaksud dengan False Positive dan False Negative?

• False positive adalah kasus dimana observasi di kelas negatif terprediksi oleh model sebagai positif. Contohnya, pasien yang sebenarnya mengidap kanker jinak, terprediksi oleh model sebagai kanker ganas.
• False negative adalah kasus dimana observasi di kelas positif terprediksi oleh model sebagai negatif. Contohnya, pasien yang sebenarnya mengidap kanker ganas, terprediksi oleh model sebagai kanker jinak.

5.4.2 Pada kasus klasifikasi, mengapa metric accuracy tidak cukup menjelaskan seberapa baik model yang diperoleh?

Untuk mengetahui seberapa baik perfomance model klasifikasi, tidak cukup dengan melihat nilai accuracy nya saja, karena accuracy menganggap sama penting untuk kasus False Positive (FP) dan False Negative (FN). Apabila kasus FP dan Kita membutuhkan metric lain seperti Precision dan Recall.

Contoh pertama: pada kasus prediksi pasien apakah mengidap kanker jinak atau ganas. Tentunya akan lebih berbahaya apabila pasien dengan kanker ganas namun terprediksi menjadi jinak. Hal ini dapat membahayakan keselamatan pasien karena tidak ditangani dengan serius oleh pihak medis. Pada kasus ini ingin diminimalisir kasus terjadinya False Negative, maka kita mengharapkan nilai Recall yang lebih tinggi dibandingkan metric lainnya.

$$Recall=\frac{TP}{TP+FN}$$

Contoh kedua: pada kasus prediksi email apakah termasuk spam atau ham (tidak spam). Akan lebih berbahaya apabila email yang sebenarnya tidak spam namun terprediksi sebagai spam. Hal ini mengakibatkan email tidak spam akan masuk ke folder spam sehingga email penting tidak terbaca oleh pengguna. Pada kasus ini ingin diminimalisir kasus False Positive, maka kita mengharapkan nilai Precision yang tinggi dibandingkan metric lainnya.

$$Precision=\frac{TP}{TP+FP}$$

Apabila kedua metric Recall dan Precision sama-sama ingin diharapkan tinggi, dapat menggunakan metric F-score yang merupakan rata-rata harmonik dari Recall dan Precision:

$$F=2\times \frac{Precision\times Recall}{Precision+Recall}$$

5.4.3 Bagaimana cara melakukan perubahan threshold pada kasus binary classification?

Secara default, fungsi predict() menggunakan nilai 0.5 sebagai threshold dalam mengklasifikasi kelas positif dan negatif. Kita dapat menggeser nilai threshold tersebut untuk mendapatkan nilai Precision-Recall yang kita inginkan.

• Semakin besar threshold, maka Precision naik, Recall turun
• Semakin kecil threshold, maka Precision turun, Recall naik

Akan lebih praktis apabila kita dapat memvisualisasikan nilai Precision-Recall untuk setiap thresholdnya. Silahkan install package cmplot yang dikembangkan oleh Ahmad Husain, salah satu instructor di Algoritma.

install.packages("remotes")
remotes::install_github("ahmadhusain/cmplot")

Membuat plot “Tradeoff model performance” dari kasus apakah sebuah SMS diklasifikasi sebagai spam (kelas positif) atau ham (not spam, kelas negatif).

library(cmplot)
confmat_plot(prob = model$predicted_prob,
             ref = model$actual_label,
             postarget = "spam",
             negtarget = "ham")

Misal dari segi bisnis dibutuhkan Precision minimal 98%, maka menurut plot di atas kita bisa set threshold 0.6324, kemudian lakukan evaluasi ulang dengan confusion matrix ataupun ROC-AUC.

threshold <- 0.6324
pred_class <- as.factor(ifelse(model$predicted_prob > threshold,
                               "spam", "ham"))

confusionMatrix(data = pred_class,
                reference = model$actual_label,
                positive = "spam")

#> Confusion Matrix and Statistics
#> 
#>           Reference
#> Prediction  ham spam
#>       ham  1215   27
#>       spam    3  148
#>                                                
#>                Accuracy : 0.9785               
#>                  95% CI : (0.9694, 0.9854)     
#>     No Information Rate : 0.8744               
#>     P-Value [Acc > NIR] : < 0.00000000000000022
#>                                                
#>                   Kappa : 0.8959               
#>                                                
#>  Mcnemar's Test P-Value : 0.00002679           
#>                                                
#>             Sensitivity : 0.8457               
#>             Specificity : 0.9975               
#>          Pos Pred Value : 0.9801               
#>          Neg Pred Value : 0.9783               
#>              Prevalence : 0.1256               
#>          Detection Rate : 0.1062               
#>    Detection Prevalence : 0.1084               
#>       Balanced Accuracy : 0.9216               
#>                                                
#>        'Positive' Class : spam                 
#> 

5.4.4 Apa kegunaan p-value pada hasil confusionmatrix dari library caret?

Digunakan untuk menguji apakah accuracy yang diperoleh lebih baik dibandingkan proporsi dari data kelas majority. Untuk lebih detailnya Anda dapat membaca referensi berikut Definition of p-value in carets confusion matrix method

Bab 6 Classification 2

6.1 Classification in General

6.1.1 Dari berbagai metode klasifikasi yang telah dipelajari, yaitu Logistic Regression, KNN, Naive Bayes, Decision Tree, dan Random Forest, bagaimana pemilihan dalam penggunaan metode tersebut?

Pemilihan metode klasifikasi bergantung pada tujuan analisis yang dilakukan. Secara umum, tujuan pemodelan klasifikasi adalah melakukan analisa terkait hubungan prediktor dengan target variabel atau melakukan prediksi.

Jika tujuannya adalah untuk melakukan analisa terkait hubungan antara prediktor dengan target variabel dapat menggunakan Logistic Regression atau Decision Tree. Berikut kelebihan dan kekurangan dari kedua metode tersebut.

Logistic Regression:

• (+) model klasifikasi yang cukup sederhana dan komputasinya cepat

• (+) interpretabilitas yang tinggi dari formula yang dibentuk

• (+) tidak memerlukan scaling data

• (+) baseline yang baik sebelum mencoba model yang lebih kompleks

• (-) perlu ketelitian saat melakukan feature engineering karena sangat bergantung pada data yang fit

• (-) tidak dapat mengevaluasi hubungan yang non-linear antara log of odds dengan prediktornya

• (-) mengharuskan antar prediktornya tidak saling berkaitan (tidak ada multikolinearitas)

  Decision Tree:

• (+) tidak memerlukan scaling data

• (+) dapat mengevaluasi hubungan yang non-linear

• (+) antar prediktornya boleh saling berkaitan

• (+) interpretabilitas dari visualisasi pohon

• (-) sangat sensitif terhadap perubahan data, sehingga cenderung tidak stabil

• (-) waktu komputasi relatif lebih lama

• (-) rentan overfitting

Jika tujuannya adalah untuk melakukan prediksi dengan harapan performa yang baik, maka dapat menggunakan Random Forest. Metode klasifikasi ini merupakan gabungan dari beberapa Decision Tree, sehingga cukup robust (tidak sensitif) terhadap outlier, antar prediktor boleh saling berkaitan, bahkan mengatasi overfitting. Namun, kekurangannya Random Forest adalah model black-box yang artinya tidak dapat diinterpretasi secara detail.

KNN digunakan ketika prediktor-prediktor numerik masuk akal ketika kita melakukan klasifikasi berdasarkan kemiripan antar observasi. Namun KNN tidak melakukan pembuatan model sehingga waktu komputasi akan lama apabila kita berhadapan dengan data yang jumlahnya besar.

Naive Bayes sangat umum digunakan ketika terdapat sangat banyak prediktor karena komputasinya yang relatif lebih cepat dibanding model lain. Misalkan pada kasus text classification, yang prediktornya merupakan kata-kata yang unique pada dataset. Berikut merupakan link eksternal yang dapat dijadikan sebagai bahan referensi The Naive Bayes Classifier

6.1.2 Bagaimana cara mengembalikan hasil prediksi berupa probability pada metode klasifikasi?

Pada dasarnya, semua metode klasifikasi akan menghasilkan nilai probability, bukan langsung kelas. Secara default, metode klasifikasi akan mengembalikan kelas dengan threshold probabilitas 0.5. Tambahkan parameter type saat melakukan predict() untuk menghasilkan nilai probability. Berikut beberapa type untuk metode klasifikasi yang dipelajari:

• type = "response" untuk Logistic Regression
• type = "raw" untuk Naive Bayes
• type = "probability" untuk Decision Tree dan Random Forest

6.1.3 Bagaimana cara handling imbalance data dengan metode SMOTE di R?

Untuk melakukan balancing data menggunakan metode SMOTE di R dapat dilakukan dengan fungsi SMOTE() dari library DMwR seperti berikut

data(iris)
data <- iris[, c(1, 2, 5)]
data$Species <- factor(ifelse(data$Species == "setosa","rare","common")) 
# checking the class distribution
prop.table(table(data$Species)) 

#> 
#>    common      rare 
#> 0.6666667 0.3333333

## now using SMOTE to create a more "balanced problem"
library(DMwR)
newData <- SMOTE(Species ~ ., data, perc.over = 600, perc.under=100)
prop.table(table(newData$Species)) 

#> 
#>    common      rare 
#> 0.4615385 0.5384615

Berikut dokumentasi dari fungsi SMOTE() SMOTE

6.2 Text Cleansing

6.2.1 Bagaimana cara menghapus stopwords dalam Bahasa Indonesia?

Daftar stopwords Bahasa Indonesia dapat diunduh terlebih dahulu melalui GitHub berikut. Import file stopwords id.txt tersebut dengan menggunakan fungsi readLines().

# import Indonesia stopwords
stop_id <- readLines("data/05-C2/stopwords_id.txt")

# generate data frame
text <- data.frame(sentence = c("saya tertarik belajar data science di @algoritma :)",
                                "anda tinggal di Jakarta",
                                "Ingin ku merat🔥 na👍",
                                "selamat tahun baru #2020 !",
                                "pingin makan yang kek gitu"))

Mengubah text berbentuk data frame ke dalam bentuk corpus dengan menggunakan fungsi VectorSource() dan VCorpus() dari library tm. Setelah itu, aplikasikan fungsi tm_map() dan removeWords() untuk menghapus stopwords dari objek stop_id.

text_clean1 <- text %>%
  pull(sentence) %>% 
  VectorSource() %>% 
  VCorpus() %>% 
  tm_map(removeWords, stop_id)

text_clean1[[1]]$content

#> [1] " tertarik belajar data science  @algoritma :)"

6.2.2 Bagaimana cara mengubah kata berimbuhan menjadi kata dasar dalam Bahasa Indonesia?

Untuk mengubah kata berimbuhan menjadi kata dasar dalam bahasa Indonesia dapat menggunakan fungsi katadasaR() dari library katadasaR. Namun, fungsi tersebut hanya menerima 1 inputan kata saja sehingga dibutuhkan fungsi sapply() untuk mengaplikasikan fungsi tersebut ke dalam 1 kalimat.

# membuat fungsi untuk mengubah kata berimbuhan menjadi kata dasar
kata_dasar <- function(x) {
  paste(sapply(words(x), katadasaR), collapse = " ")
  }

Menggunakan fungsi di atas dengan menggabungkan fungsi tm_map() dan content_transformer().

text_clean2 <- text %>%
  pull(sentence) %>% 
  VectorSource() %>% 
  VCorpus() %>% 
  tm_map(content_transformer(kata_dasar))

text_clean2[[1]]$content

#> [1] "saya tarik ajar data science di @algoritma :)"

6.2.3 Bagaimana cara menghapus emoticon dan emoji?

Untuk menghapus emoticon dan emoji dapat menggunakan fungsi replace_emoji() dan replace_emoticon() dari library textclean. Kedua fungsi tersebut hanya menerima kalimat dengan tipe data berupa karakter, sehingga harus diubah terlebih dahulu tipe datanya jika masih belum karakter.

text_clean3 <- text %>%
  mutate(sentence = as.character(sentence)) %>% 
  pull(sentence) %>% 
  replace_emoji() %>% 
  replace_emoticon()

text_clean3

#> [1] "saya tertarik belajar data science di @algoritma smiley "
#> [2] "anda tinggal di Jakarta"                                 
#> [3] "Ingin ku merat<U+0001F525> na<U+0001F44D>"               
#> [4] "selamat tahun baru #2020 !"                              
#> [5] "pingin makan yang kek gitu"

6.2.4 Bagaimana cara menghapus mention dan hashtag?

Untuk menghapus mention dan hashtag dapat menggunakan fungsi replace_hash() dan replace_tag() dari library textclean.

text_clean4 <- text %>%
  mutate(sentence = as.character(sentence)) %>% 
  pull(sentence) %>% 
  replace_hash() %>% 
  replace_tag()

text_clean4

#> [1] "saya tertarik belajar data science di  :)"
#> [2] "anda tinggal di Jakarta"                  
#> [3] "Ingin ku merat<U+0001F525> na<U+0001F44D>"
#> [4] "selamat tahun baru  !"                    
#> [5] "pingin makan yang kek gitu"

6.2.5 Bagaimana cara menghapus slang words dalam Bahasa Indonesia?

Daftar slang words Bahasa Indonesia dapat diunduh terlebih dahulu melalui GitHub berikut.

slang_id <- read.csv("data/05-C2/colloquial-indonesian-lexicon.csv") 

Untuk menghapus slang words dapat menggunakan fungsi replace_internet_slang() dari library textclean.

text_clean5 <- text %>%
  mutate(sentence = as.character(sentence)) %>% 
  pull(sentence) %>%
  replace_internet_slang(slang = paste0('\\b', slang_id$slang, '\\b') , 
                         replacement = slang_id$formal, 
                         ignore.case = T)

text_clean5

#> [1] "saya tertarik belajar data science di @algoritma :)"
#> [2] "anda tinggal di Jakarta"                            
#> [3] "Ingin ku merat<untuk+0001F525> nya<untuk+0001F44D>" 
#> [4] "selamat tahun baru #2020 !"                         
#> [5] "pengin makan yang kayak begitu"

Berikut link eksternal yang dapat dijadikan sebagai bahan referensi dalam melakukan cleaning text:

• Text Cleaning Bahasa Indonesia
• Text Cleaning Bahasa Inggris

6.2.6 Selain proses stemming apakah bisa menggunakan lemmatization untuk memisahkan kata dasar dengan imbuhan?

Proses stemming bertujuan untuk menghilangkan imbuhan dari suatu kata berimbuhan. Pada stemming bahasa inggris misalnya fungsi stemming akan menghapus suku kata d, ed, s, es, ing, etc. Sehingga, ada kemungkinan terdapat kata-kata yang hasil stemmingnya kurang tepat seperti “balance”. Namun, hal ini tidak akan berpengaruh terhadap hasil pemodelan karena kata yang dihasilkan sama/seragam (dianggap sebagai satu prediktor yang sama). Hal ini karena komputer/machine learning tidak memahami/mengerti konteks/makna dari kata tersebut. Namun, hal ini akan cukup menggangu ketika melakukan visualisasi seperti membuat wordcloud.

Solusinya dapat mencoba alternatif lain, yaitu lemmatization. Berbeda dengan stemming, lemmatization dapat memisahkan kata dasar dengan kata imbuhannya secara tepat. Hal ini karena, secara sederhana lemmatization bekerja seperti ketika kita menghapus stopwords, dimana kita sebenarnya mempunyai kamus besar yang berisi berbagai macam jenis kata berimbuhan dan kata dasarnya.

Penjelasan secara detail tentang stemming dan lemmatization dapat dibaca melalui Stemming and lemmatization dan textstem package

6.2.7 Bagaiaman proses tokenization untuk pasangan kata?

Tokenization pasangan kata, seperti “saya pergi”, “tidak suka”, etc. adalah salah satu tahapan yang umum dilakukan di n-gram analysis (bigram analysis bila terdapat 2 pasangan kata). Hal tersebut umumnya dilakukan pada kasus analisis korelasi antar kata. Berikut beberapa artikel yang mengaplikasikan proses tokenization pasangan kata:

• 4 Relationships between words: n-grams and correlations
• TEXT GENERATION WITH MARKOV CHAINS
• Topic Modelling with LDA

6.3 Naive Bayes

6.3.1 Apakah metode Naive Bayes dapat diterapkan untuk prediktor bertipe numerik?

Naive bayes dapat diterapkan pada berbagai permasalahan klasifikasi, tidak terbatas pada klasifikasi text. Jika prediktor yang digunakan bertipe numerik, Naive Bayes akan menghitung rata-rata (mean) dan standard deviation (sd) untuk setiap level target. Peluang didapatkan dengan mengasumsikan bahwa prediktor numerik memiliki distribusi normal. Tipe Naive Bayes ini disebut sebagai Gaussian Naive Bayes. Berikut contoh naive bayes pada data iris.

naiveBayes(Species ~ ., iris)

#> 
#> Naive Bayes Classifier for Discrete Predictors
#> 
#> Call:
#> naiveBayes.default(x = X, y = Y, laplace = laplace)
#> 
#> A-priori probabilities:
#> Y
#>     setosa versicolor  virginica 
#>  0.3333333  0.3333333  0.3333333 
#> 
#> Conditional probabilities:
#>             Sepal.Length
#> Y             [,1]      [,2]
#>   setosa     5.006 0.3524897
#>   versicolor 5.936 0.5161711
#>   virginica  6.588 0.6358796
#> 
#>             Sepal.Width
#> Y             [,1]      [,2]
#>   setosa     3.428 0.3790644
#>   versicolor 2.770 0.3137983
#>   virginica  2.974 0.3224966
#> 
#>             Petal.Length
#> Y             [,1]      [,2]
#>   setosa     1.462 0.1736640
#>   versicolor 4.260 0.4699110
#>   virginica  5.552 0.5518947
#> 
#>             Petal.Width
#> Y             [,1]      [,2]
#>   setosa     0.246 0.1053856
#>   versicolor 1.326 0.1977527
#>   virginica  2.026 0.2746501

6.4 Tree-based Model

6.4.1 Apa yang dimaksud dengan ensemble method?

Ensemble method merupakan gabungan prediksi dari beberapa model menjadi prediksi tunggal. Random forest merupakan salah satu jenis ensemble method untuk kasus klasifikasi yang memanfaatkan konsep Bagging, yaitu gabungan dari Bootstrap dan Aggregation.

• Bootstrap merupakan proses pengambilan sampel dengan pengembalian, adanya pengembalian memiliki kemungkinan data yang diambil berulang (baris terduplikasi). Setiap observasi memiliki peluang yang sama untuk dijadikan sampel.

• Aggregation, dari beberapa model yang telah terbentuk dikumpulkan semua hasil prediksi untuk menentukan hasil prediksi tunggal. Untuk klasifikasi, maka dilakukan majority voting dimana kelas yang paling banyak diprediksi akan menjadi targetnya. Sedangkan untuk regresi akan diperoleh nilai rata-rata targetnya dari setiap model.

6.4.2 Secara default, Random Forest akan membangun sebanyak 500 tree. Bagaimana cara mengubahnya?

Gunakan parameter ntree pada fungsi train(). Misalnya kita hanya ingin membuat 100 trees, agar komputasinya lebih cepat. Pada finalModel kita dapat lihat bahwa Number of trees yang dipakai adalah 100.

set.seed(100)
diab_forest_100 <- train(diabetes ~ .,
                         data = diab,
                         method = "rf",
                         ntree = 100)

diab_forest_100$finalModel$param

#> $ntree
#> [1] 100

6.4.3 Secara default, Random Forest akan mencoba 3 nilai mtry. Bagaimana cara mengubahnya?

Gunakan parameter tuneGrid pada fungsi train() dengan menyiapkan dataframe dari expand.grid() berupa daftar kemungkinan nilai dari parameter mtry. Misalkan saya hanya ingin Random Forest yang menggunakan mtry 4 dan 5:

grid <- expand.grid(mtry = c(4, 5))
grid

#>   mtry
#> 1    4
#> 2    5

set.seed(100)
diab_forest_tune <- train(diabetes ~ .,
                          data = diab,
                          method = "rf",
                          tuneGrid = grid)

diab_forest_tune

#> Random Forest 
#> 
#> 768 samples
#>   8 predictor
#>   2 classes: 'neg', 'pos' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (25 reps) 
#> Summary of sample sizes: 768, 768, 768, 768, 768, 768, ... 
#> Resampling results across tuning parameters:
#> 
#>   mtry  Accuracy   Kappa    
#>   4     0.7539355  0.4467487
#>   5     0.7552129  0.4498807
#> 
#> Accuracy was used to select the optimal model using the largest value.
#> The final value used for the model was mtry = 5.

6.4.4 Secara default, Random Forest akan memilih model dengan Accuracy terbaik. Bagaimana cara mengubahnya agar menggunakan metric Precision atau Recall atau bahkan AUC?

Terdapat parameter pada fungsi trainControl():

• summaryFunction = prSummary untuk menghitung nilai precision-recall
• classProbs = TRUE untuk perhitungan nilai AUC

Kemudian gunakan parameter metric pada fungsi train() untuk memilih metric mana yang ingin diunggulkan: "AUC", "Precision", "Recall", atau "F". Misalkan untuk kasus prediksi diabetes, karena ingin meminimalisir kasus False Negative berarti kita berharap untuk mendapatkan model dengan metric Recall tertinggi.

set.seed(100)
ctrl <- trainControl(summaryFunction = prSummary,
                     classProbs = TRUE)

diab_forest_pr <- train(diabetes ~ .,
                        data = diab,
                        method = "rf",
                        trControl = ctrl,
                        metric = "Recall")

diab_forest_pr

#> Random Forest 
#> 
#> 768 samples
#>   8 predictor
#>   2 classes: 'neg', 'pos' 
#> 
#> No pre-processing
#> Resampling: Bootstrapped (25 reps) 
#> Summary of sample sizes: 768, 768, 768, 768, 768, 768, ... 
#> Resampling results across tuning parameters:
#> 
#>   mtry  AUC        Precision  Recall     F        
#>   2     0.8855808  0.8011553  0.8435644  0.8211170
#>   5     0.8642503  0.8055431  0.8294605  0.8165980
#>   8     0.8412353  0.7993967  0.8226283  0.8101388
#> 
#> Recall was used to select the optimal model using the largest value.
#> The final value used for the model was mtry = 2.

6.4.5 Bagaimana implementasi model regresi pada Random Forest?

Import data yang akan digunakan:

insurance <- read.csv("data/05-C2/insurance.csv")
head(insurance)

#>   age    sex    bmi children smoker    region   charges
#> 1  19 female 27.900        0    yes southwest 16884.924
#> 2  18   male 33.770        1     no southeast  1725.552
#> 3  28   male 33.000        3     no southeast  4449.462
#> 4  33   male 22.705        0     no northwest 21984.471
#> 5  32   male 28.880        0     no northwest  3866.855
#> 6  31 female 25.740        0     no southeast  3756.622

Lakukan cross validation dengan fungsi initial_split pada library rsample:

set.seed(100)
idx <- initial_split(insurance, prop = 0.8)

# check train dataset
train <- training(idx) 

# check test dataset
test <- testing(idx) 

Cara membuat model regresi dengan Random Forest tidak berbeda dengan kasus klasifikasi, ketika target variabel yang digunakan bertipe numerik, otomatis model akan menghasilkan model regresi.

set.seed(100)
ctrl <- trainControl(method = "repeatedcv",
                     number = 5,
                     repeats = 3)

insurance_forest <- train(charges ~ .,
                          data = train,
                          method = "rf",
                          trControl = ctrl)

insurance_forest

#> Random Forest 
#> 
#> 857 samples
#>   6 predictor
#> 
#> No pre-processing
#> Resampling: Cross-Validated (5 fold, repeated 3 times) 
#> Summary of sample sizes: 685, 686, 685, 687, 685, 685, ... 
#> Resampling results across tuning parameters:
#> 
#>   mtry  RMSE      Rsquared   MAE     
#>   2     5478.898  0.8335458  3708.914
#>   5     4822.793  0.8433103  2729.368
#>   8     4944.418  0.8365218  2827.233
#> 
#> RMSE was used to select the optimal model using the smallest value.
#> The final value used for the model was mtry = 5.

Melakukan prediksi pada data test dan evaluasi model menggunakan nilai RMSE:

test$pred <- predict(object = insurance_forest, newdata = test)
RMSE(y_pred = test$pred, y_true = test$charges)

#> [1] 3891.623

6.5 Model Evaluation

6.5.1 Jelaskan kegunaan dari ROC dan AUC?

Kurva ROC (Receiver Operating Characteristic) menggambarkan seberapa baik kinerja model klasifikasi biner. Kurva ROC dibentuk dari nilai TPR (True Positive Rate) dan FPR (False Positive Rate) untuk semua nilai threshold dari 0 hingga 1. AUC (Area Under the Curve) adalah luas daerah dari kurva ROC. Nilai AUC mendekati 1 artinya model sangat baik, ketika nilai AUC berada di sekitar 0.5 maka model tersebut memiliki performance yang tidak baik dan hanya menebak secara random.

6.5.2 Apakah k-fold cross validation dapat digunakan untuk metode klasifikasi selain Random Forest?

k-fold cross validation dapat digunakan untuk semua metode klasifikasi bahkan di luar metode yang telah dipelajari. Namun, karena k-fold cross validation tidak memperlihatkan hasil pemodelan untuk semua subset data (hanya mengambil model dengan performa terbaik), maka tetap perlu dilakukan cross validation untuk melakukan evaluasi model. Berikut contoh k-fold cross validation untuk metode Decision Tree:

set.seed(417)
ctrl <- trainControl(method = "repeatedcv", number = 5, repeats = 3)
# parameter method dapat disesuaikan dengan metode klasifikasi yang digunakan
model <- train(attrition ~ .,
               data = train,
               method = "ctree",
               trControl = ctrl)

6.6 Mathematics Concept

6.6.1 Bayes Theorem

6.6.2 Independent Event

Ketika ada 2 kejadian yang terjadi secara bersamaan, peluang satu kejadian tidak mempengaruhi kejadian yang lain. Maka, peluang terjadi 2 kejadian yang tidak saling berhubungan adalah hasil perkalian masing-masing peluang kejadian tersebut.

$$P(A\cap B)=P\left(A\right)P\left(B\right)$$

6.6.3 Dependent Event

Peluang satu kejadian dipengaruhi atau berubah sesuai dengan informasi tentang kejadian lainnya. Untuk menghitung peluangnya, kita bisa menggunakan Bayes Theorem.

$$P\left(A|B\right)=\frac{P\left(B|A\right)P\left(A\right)}{P\left(B\right)}=\frac{P\left(B|A\right)P\left(A\right)}{P\left(B|A\right)P\left(A\right)+P\left(B|\neg A\right)P\left(\neg A\right)}$$

• $P\left(A|B\right)$: Peluang terjadi A apabila diketahui B telah terjadi.
• $P\left(B|A\right)$: Peluang terjadi B apabila diketahui A telah terjadi.
• $P\left(B|\neg A\right)$: Peluang terjadi B apabila diketahui A tidak terjadi.
• $P\left(A\right)$: Peluang terjadi A
• $P\left(\neg A\right)$: Peluang tidak terjadi A

6.6.4 Entropy

Entropy adalah ukuran ketidakteraturan (measure of disorder) yang bisa digunakan untuk mewakili seberapa beragam kelas yang ada dalam suatu variabel.

$$Entropy={\Sigma }_{i=1}^c-p_{i}lo{g}_2{p}_i$$

Nilai entropy apabila dalam satu variabel terdapat 2 kelas atau nilai:

$$Entropy=-p_{1}lo{g}_2{p}_1-p_{2}lo{g}_2{p}_2$$

• $p_i$: proporsi kelas ke-i (jumlah observasi kelas i dibagi total seluruh observasi)

6.6.5 Information Gain

Information Gain digunakan untuk mengukur perubahan Entropy dan tingkat keragaman kelas setelah dilakukan percabangan. Ketika kita memisahkan 1 data menjadi 2 cabang menggunakan variabel tertentu, information gain dipakai untuk menentukan variabel mana yang dapat memberikan penurunan Entropy yang paling besar.

$$InformationGain=Entropy\left(awal\right)-(P_{1}Entrop{y}_1+P_{2}Entrop{y}_2)$$

• $P_1$: proporsi data pada cabang kiri
• $Entrop{y}_1$: nilai entropy pada cabang kiri
• $P_2$: proporsi data pada cabang kanan
• $Entrop{y}_2$: nilai entropy pada cabang kanan

Untuk mencari variabel terbaik yang bisa digunakan untuk memisahkan dua kelas supaya entropy-nya semakin kecil, kita cari nilai Information Gain untuk tiap variabel dan pilih variable yang memberikan Information Gain terbesar sebagai percabangannya.

6.6.6 Gini Index

Gini index adalah alternatif dari nilai Entropy. Secara komputasi, Gini lebih cepat dibandingkan Entropy karena hanya berupa perkalian, sedangkan Entropy menggunakan fungsi logaritma.

$$Gini={\Sigma }_{i=1}^{C}p\left(i\right)(1-p(i\left)\right)$$

Sehingga Gini untuk 2 kelas:

$$Gini=p\left(a\right)(1-p(a\left)\right)+p\left(b\right)(1-p(b\left)\right)$$

6.6.7 Variable Importance

Variable Importance yang dihitung oleh Random Forest didapatkan dari rumus Gini Importance, yang konsepnya sama dengan Information Gain. Namun Gini Importance menggunakan Gini Index, bukan nilai Entropy.

$$GiniImportance=Gin{i}_{awal}-(P_{1}Gin{i}_1+P_{2}Gin{i}_2)$$

6.6.8 ROC Curve

Berikut ini ilustrasi yang menggambarkan kondisi ROC (Receiver Operating characteristic) Curve yang diinginkan ketika kelas imbalance adalah mendapatkan True Positive setinggi mungkin dan False Positive serendah mungkin.

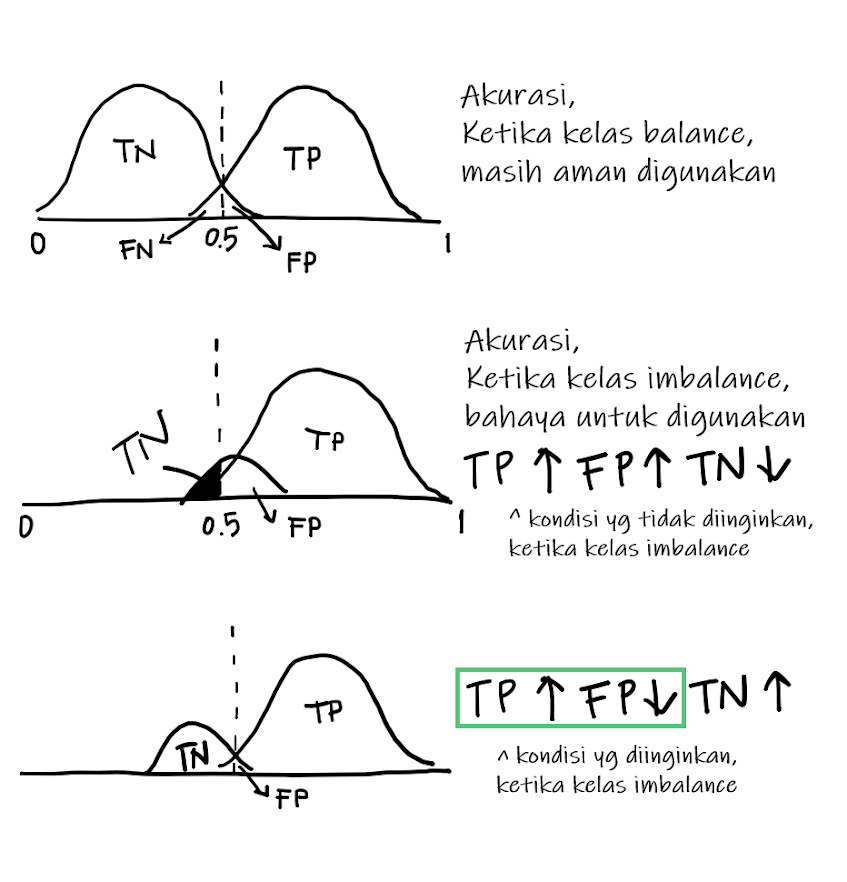
Bab 7 Unsupervised Learning

7.1 PCA: Dimensionality Reduction

7.1.1 Permasalahan apa yang terdapat pada data berdimensi tinggi?

• menyulitkan pengolahan data
• memerlukan komputasi yang besar
• tidak efisien secara waktu

7.1.2 Perbedaan membuat PCA dengan menggunakan fungsi prcomp() dan PCA() dari library FactoMineR?

Fungsi untuk membuat biplot di R:

• biplot(prcomp()) -> base R
• plot.PCA(PCA()) -> package FactoMineR

Kelebihan ketika membuat PCA dengan menggunakan fungsi PCA() dari library FactoMineR adalah bisa membuat biplot lebih spesifik:

• memisahkan dua grafik yang terdapat pada biplot yaitu individual factor map dan variables factor map
• mengkombinasikan antara variabel numerik dan kategorik dengan menggunakan fungsi plot.PCA().

7.1.3 Apakah terdapat best practice dalam menentukan jumlah PC yang digunakan pada PCA?

Penentuan jumlah PC yang digunakan bergantung pada kebutuhan analisa yang dilakukan. Namun, kembali pada tujuan awal melakukan PCA, yaitu untuk mereduksi dimensi supaya analisis lanjutan yang dilakukan memiliki waktu yang relatif cepat dan ruang penyimpanan yang lebih efisien. Sehingga, seringkali seorang analis menentapkan threshold lebih dari 70-75% informasi. Maksudnya jumlah PC yang digunakan adalah jumlah PC yang sudah merangkum kurang lebih 70-75% informasi. Namun, threshold tersebut sifatnya tidak mutlak artinya disesuaikan dengan kebutuhan analisis dan bisnis. Berikut merupakan link eksternal yang dapat dijadikan sebagai bahan referensi How many components can I retrieve in principal component analysis?.

7.1.4 Bagaimana implementasi PCA pada data pre-processing?

Berikut ini adalah implementasi PCA pada tahapan data pre-processing dengan menggunakan data attrition.

attrition <- read.csv("data/06-UL/attrition.csv")
str(attrition)

#> 'data.frame':	1470 obs. of  35 variables:
#>  $ attrition                 : chr  "yes" "no" "yes" "no" ...
#>  $ age                       : int  41 49 37 33 27 32 59 30 38 36 ...
#>  $ business_travel           : chr  "travel_rarely" "travel_frequently" "travel_rarely" "travel_frequently" ...
#>  $ daily_rate                : int  1102 279 1373 1392 591 1005 1324 1358 216 1299 ...
#>  $ department                : chr  "sales" "research_development" "research_development" "research_development" ...
#>  $ distance_from_home        : int  1 8 2 3 2 2 3 24 23 27 ...
#>  $ education                 : int  2 1 2 4 1 2 3 1 3 3 ...
#>  $ education_field           : chr  "life_sciences" "life_sciences" "other" "life_sciences" ...
#>  $ employee_count            : int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ employee_number           : int  1 2 4 5 7 8 10 11 12 13 ...
#>  $ environment_satisfaction  : int  2 3 4 4 1 4 3 4 4 3 ...
#>  $ gender                    : chr  "female" "male" "male" "female" ...
#>  $ hourly_rate               : int  94 61 92 56 40 79 81 67 44 94 ...
#>  $ job_involvement           : int  3 2 2 3 3 3 4 3 2 3 ...
#>  $ job_level                 : int  2 2 1 1 1 1 1 1 3 2 ...
#>  $ job_role                  : chr  "sales_executive" "research_scientist" "laboratory_technician" "research_scientist" ...
#>  $ job_satisfaction          : int  4 2 3 3 2 4 1 3 3 3 ...
#>  $ marital_status            : chr  "single" "married" "single" "married" ...
#>  $ monthly_income            : int  5993 5130 2090 2909 3468 3068 2670 2693 9526 5237 ...
#>  $ monthly_rate              : int  19479 24907 2396 23159 16632 11864 9964 13335 8787 16577 ...
#>  $ num_companies_worked      : int  8 1 6 1 9 0 4 1 0 6 ...
#>  $ over_18                   : chr  "y" "y" "y" "y" ...
#>  $ over_time                 : chr  "yes" "no" "yes" "yes" ...
#>  $ percent_salary_hike       : int  11 23 15 11 12 13 20 22 21 13 ...
#>  $ performance_rating        : int  3 4 3 3 3 3 4 4 4 3 ...
#>  $ relationship_satisfaction : int  1 4 2 3 4 3 1 2 2 2 ...
#>  $ standard_hours            : int  80 80 80 80 80 80 80 80 80 80 ...
#>  $ stock_option_level        : int  0 1 0 0 1 0 3 1 0 2 ...
#>  $ total_working_years       : int  8 10 7 8 6 8 12 1 10 17 ...
#>  $ training_times_last_year  : int  0 3 3 3 3 2 3 2 2 3 ...
#>  $ work_life_balance         : int  1 3 3 3 3 2 2 3 3 2 ...
#>  $ years_at_company          : int  6 10 0 8 2 7 1 1 9 7 ...
#>  $ years_in_current_role     : int  4 7 0 7 2 7 0 0 7 7 ...
#>  $ years_since_last_promotion: int  0 1 0 3 2 3 0 0 1 7 ...
#>  $ years_with_curr_manager   : int  5 7 0 0 2 6 0 0 8 7 ...

Sebelum melakukan PCA terlebih dahulu dilakukan cross validation, yaitu membagi data menjadi training set untuk proses pemodelan dan testing set untuk melakukan evaluasi. Namun, data train dan data test tidak langsung dimasukkan ke dalam sebuah objek melainkan dilakukan PCA terlebih dahulu.

Cross validation akan dilakukan dengan menggunakan fungsi initial_split() dari library rsample. Fungsi tersebut akan melakukan proses sampling untuk cross validation dengan metode stratified random sampling, sehingga proporsi target variabel pada data awal, akan dipertahankan baik pada training set maupun testing set.

set.seed(417)
splitted <- initial_split(data = attrition,
                          prop = 0.8,
                          strata = "attrition")
splitted

#> <Analysis/Assess/Total>
#> <1177/293/1470>

Melakukan tahapan data preparation yang didalamnya termasuk melakukan PCA. Data preparation yang akan dilakukan adalah menghapus variabel yang dianggap tidak berpengaruh, membuang variabel yang variansinya mendekati 0 (tidak informatif), melakukan scaling, dan melakukan PCA. Proses yang dilakukan pada tahapan data preparation akan dilakukan dengan menggunakan fungsi dari library recipes, yaitu:

• step_rm() untuk menghapus variabel
• step_nzv() untuk membuang variabel yang variansinya mendekati 0
• step_center() dan step_scale() untuk melakukan scaling
• step_pca() untuk melakukan PCA

rec <- recipe(attrition ~ ., training(splitted)) %>% 
  step_rm(employee_count, employee_number) %>%
  step_nzv(all_predictors()) %>% 
  step_center(all_numeric()) %>% 
  step_scale(all_numeric()) %>% 
  step_pca(all_numeric(), threshold = 0.8) %>% 
  prep()

Setelah mendefinisikan proses data preparation pada objek rec, selanjutnya proses tersebut diterapkan ke data train menggunakan fungsi juice() dan ke data test menggunakan fungsi bake() dari library recipes.

train <- juice(rec)
head(train, 5)

#> # A tibble: 5 x 21
#>   business_travel department education_field gender job_role marital_status
#>   <fct>           <fct>      <fct>           <fct>  <fct>    <fct>         
#> 1 travel_rarely   sales      life_sciences   female sales_e~ single        
#> 2 travel_frequen~ research_~ life_sciences   male   researc~ married       
#> 3 travel_rarely   research_~ other           male   laborat~ single        
#> 4 travel_frequen~ research_~ life_sciences   female researc~ married       
#> 5 travel_rarely   research_~ medical         male   laborat~ married       
#> # ... with 15 more variables: over_time <fct>, attrition <fct>, PC01 <dbl>,
#> #   PC02 <dbl>, PC03 <dbl>, PC04 <dbl>, PC05 <dbl>, PC06 <dbl>, PC07 <dbl>,
#> #   PC08 <dbl>, PC09 <dbl>, PC10 <dbl>, PC11 <dbl>, PC12 <dbl>, PC13 <dbl>

test <- bake(rec, testing(splitted))
head(test, 5)

#> # A tibble: 5 x 21
#>   business_travel department education_field gender job_role marital_status
#>   <fct>           <fct>      <fct>           <fct>  <fct>    <fct>         
#> 1 travel_rarely   research_~ medical         female laborat~ married       
#> 2 travel_rarely   research_~ life_sciences   male   laborat~ divorced      
#> 3 travel_rarely   research_~ medical         male   healthc~ married       
#> 4 travel_rarely   research_~ medical         male   laborat~ divorced      
#> 5 travel_rarely   research_~ life_sciences   male   laborat~ single        
#> # ... with 15 more variables: over_time <fct>, attrition <fct>, PC01 <dbl>,
#> #   PC02 <dbl>, PC03 <dbl>, PC04 <dbl>, PC05 <dbl>, PC06 <dbl>, PC07 <dbl>,
#> #   PC08 <dbl>, PC09 <dbl>, PC10 <dbl>, PC11 <dbl>, PC12 <dbl>, PC13 <dbl>

Dari output di atas diketahui bahwa variabel numerik sudah berbentuk sebuah PC. Selanjutnya, data sudah siap dilanjutkan ke tahap modeling.

7.1.5 Bagaimana penerapan PCA di industri?

PCA pada industri lebih sering digunakan untuk data preparation sama halnya seperti scaling, feature engineering, ataupun feature selection. PCA digunakan untuk mereduksi data berdimensi besar besar menjadi lebih kecil, secara sederhana dapat dikatakan mengurangi jumlah kolom pada data. Walaupun begitu, PCA tetap mempertahankan informasi dari semua variabel. Sebelum mereduksi dimensi, PCA akan merangkum terlebih dahulu semua informasi yang terdapat pada setiap variabel ke dalam bentuk PC, PC tersebut yang nantinya akan direduksi (dikurangi) dimensinya. Oleh karena itu, variabel yang digunakan jumlahnya tetap sama seperti data awal, hanya informasi (variansinya) saja yang berkurang. Berikut merupakan link eksternal yang dapat dijadikan sebagai bahan referensi An Application of PCA.

Contoh permasalahan yang sering ditemui adalah klasifikasi dokumen. Saat ini semua administrasi dilakukan secara online/elektronik (tidak manual), adakalanya seorang nasabah/pelamar/customer harus melakukan upload dokumen. Sebelum adanya klasifikasi dokumen, pemeriksaan kebenaran dokumen dilakukan secara manual sehingga membutuhkan waktu yang cukup lama dan kapasitas penyimpanan yang relatif besar karena aplikasi tidak mampu memilah mana dokumen yang sudah sesuai dan mana yang belum. Namun, permasalahan tersebut sudah mampu terjawab dengan adanya klasifikasi dokumen. Data untuk klasifikasi dokumen adalah data image yang jika dilakukan proses klasifikasi akan memerlukan komputasi yang relatif lama dibandingkan data tabular biasa. Oleh karena itu, perlu dilakukan PCA untuk mereduksi dimensi data image tersebut supaya komputasi saat proses klasifikasi bisa menjadi lebih cepat. Berikut merupakan link eksternal yang dapat dijadikan sebagai bahan referensi Image Compression with PCA in R.

7.2 PCA: Visualization

7.2.1 Apakah biplot dapat menampilkan PC lain selain PC1 dan PC2?

Bisa, tetapi informasi yang dijelaskan menjadi berkurang, karena secara default PC1 dan PC2 merangkum informasi paling banyak. Berikut contoh membuat biplot dengan menggunakan PC lain (selain PC1 dan PC2):

head(USArrests)

#>            Murder Assault UrbanPop Rape
#> Alabama      13.2     236       58 21.2
#> Alaska       10.0     263       48 44.5
#> Arizona       8.1     294       80 31.0
#> Arkansas      8.8     190       50 19.5
#> California    9.0     276       91 40.6
#> Colorado      7.9     204       78 38.7

Membuat PCA dari data USArrests dengan menggunakan fungsi prcomp().

pca_us <- prcomp(USArrests, scale = T)

Membuat visualisasi dari hasil PCA dengan menggunakan fungsi biplot().

# parameter `choices` dapat diganti sesuai PC yang ingin dibuat, secara default menggunakan  PC1 dan PC2 (choices = 1:2)
biplot(pca_us, choices = 2:3)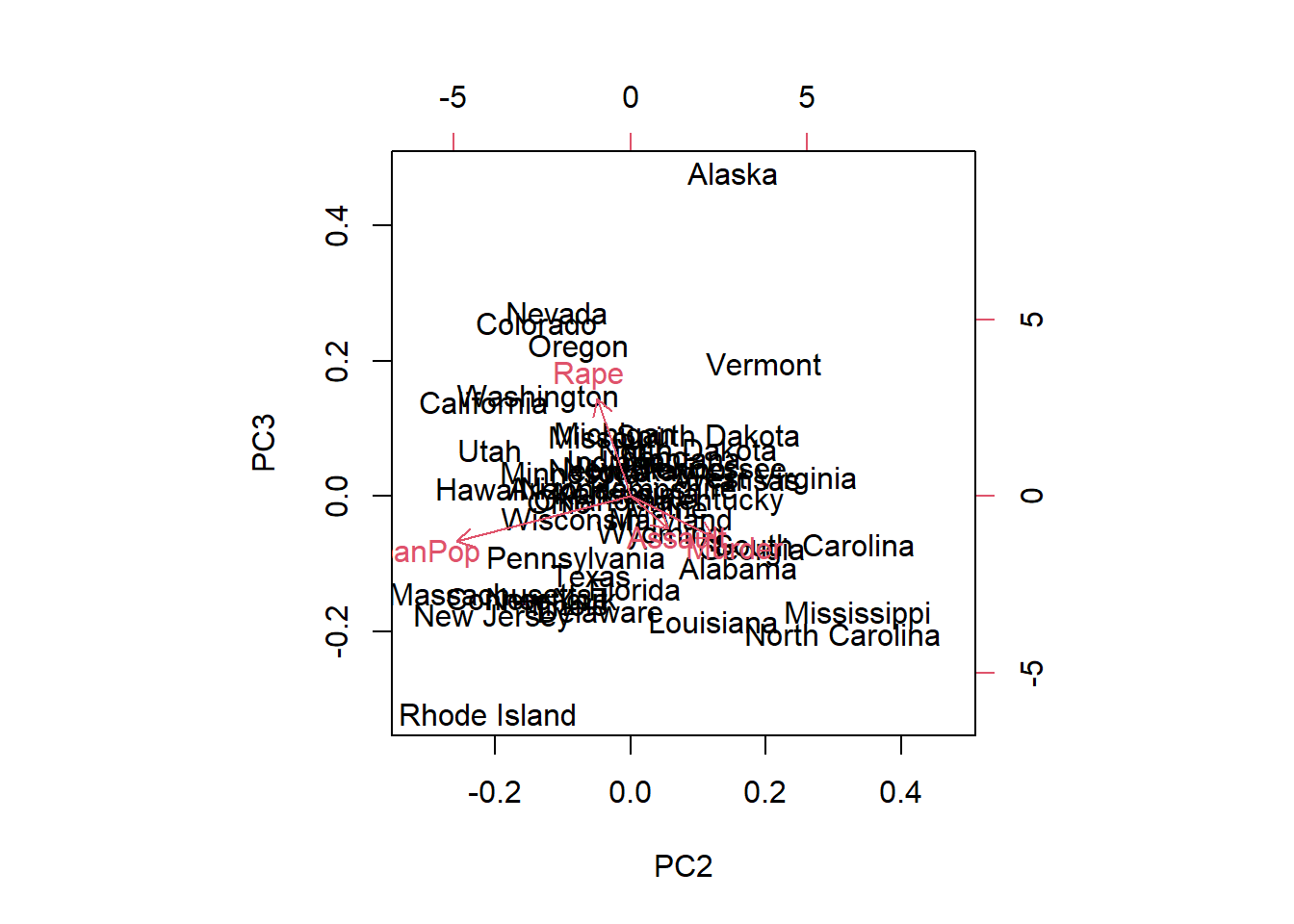

7.2.2 Apakah kita dapat memvisualisasikan biplot dengan 3 dimensi?

Untuk menampilkan biplot dengan 3 dimensi dapat menggunakan function plot_ly() dari package plotly. Berikut ini akan dicontohkan memvisualisasikan biplot dari PC1, PC2, PC3 dan juga akan dibedakan setiap titik observasi dengan cluster nya. Sebelum masuk ke visualisasi, akan dicari terlebih dahulu cluster untuk setiap observasi.

# Read data in
whiskies <- read.csv("data/06-UL/whiskies.txt")

# Distillery column is the name of each whisky
rownames(whiskies) <- whiskies[,"Distillery"]

# remove RowID, Postcode, Latitude and Longitude
whiskies <- whiskies[,3:14]

# k-means clustering
whi_km <- kmeans(scale(whiskies), 4)

Setelah menggunakan kmeans() untuk mendapatkan cluster, berikutnya kita lakukan PCA dan membentuk PC yang diperoleh dalam bentuk data frame.

whis.pca <- PCA(whiskies, graph = F, scale.unit = T)
df_pca <- data.frame(whis.pca$ind$coord) %>% 
          bind_cols(cluster = as.factor(whi_km$cluster))
head(df_pca)

#>                   Dim.1      Dim.2      Dim.3      Dim.4       Dim.5 cluster
#> Aberfeldy   -0.65565655  1.2056463 -0.1663438 -0.7807432  0.14526590       1
#> Aberlour    -2.31263102  3.7479878  1.3669186  0.8719922  0.69366566       1
#> AnCnoc      -1.60215288 -0.6640822 -0.2972053 -1.1027897 -0.01535638       4
#> Ardbeg       5.41363278  0.2448746  1.2101422 -0.7483052 -0.19536723       3
#> Ardmore      0.12164922  0.4127927 -0.3044621 -1.2705758  1.49597271       2
#> ArranIsleOf  0.09941062 -1.3966133 -1.2024542  1.6549138 -0.28659985       4

Visualisasikan PC dan membedakan warna tiap observasi berdasarkan clusternya.

plot_ly(df_pca, x = ~Dim.1, y = ~Dim.2, z = ~Dim.3, color = ~cluster)

7.2.3 Bagaimana implementasi visualisasi PCA menggunakan package factoextra?

Kita akan mencoba melakukan visualisasi pada data setelah dilakukan PCA dengan menggunakan data loan.

loan <- read.csv("data/06-UL/loan2017Q4.csv")
str(loan)

#> 'data.frame':	1556 obs. of  16 variables:
#>  $ initial_list_status: chr  "w" "f" "w" "w" ...
#>  $ purpose            : chr  "debt_consolidation" "debt_consolidation" "debt_consolidation" "debt_consolidation" ...
#>  $ int_rate           : num  14.08 9.44 28.72 13.59 15.05 ...
#>  $ installment        : num  676 480 1010 484 476 ...
#>  $ annual_inc         : num  156700 50000 25000 175000 109992 ...
#>  $ dti                : num  19.1 19.4 65.6 12.6 10 ...
#>  $ verification_status: chr  "Source Verified" "Not Verified" "Verified" "Not Verified" ...
#>  $ grade              : chr  "C" "B" "F" "C" ...
#>  $ revol_bal          : int  21936 5457 23453 31740 2284 2016 14330 27588 27024 11719 ...
#>  $ inq_last_12m       : int  3 1 0 0 3 5 0 1 8 1 ...
#>  $ delinq_2yrs        : int  0 1 0 0 0 0 0 0 0 0 ...
#>  $ home_ownership     : chr  "MORTGAGE" "RENT" "OWN" "MORTGAGE" ...
#>  $ not_paid           : int  0 1 1 1 0 1 0 1 1 0 ...
#>  $ log_inc            : num  12 10.8 10.1 12.1 11.6 ...
#>  $ verified           : int  1 0 1 0 0 0 0 0 1 1 ...
#>  $ grdCtoA            : int  0 1 0 0 0 1 0 1 0 0 ...

Sebelum melakukan PCA kita akan melakukan tahapan data preparation terlebih dahulu dengan membuang variabel initial_list_status, home_ownership, dan not_paid karena visualisasi yang akan dibuat tidak memerlukan insight dari ketiga variabel tersebut.

loan_clean <- loan %>% 
  select(-c(initial_list_status, home_ownership, not_paid))

Membuat PCA dengan menggunakan fungsi PCA() dari library FactoMineR. Parameter yang digunakan adalah:

• ncp: Jumlah PC yang akan dihasilkan. Secara default fungsi PCA() hanya akan menampilkan 5 PC awal (5 PC yang merangkum informasi paling banyak)
• quali.sup: Nomor kolom dari variabel kategorik
• graph: Sebuah logical value. T akan menampilkan hasil visualisasi, F tidak menampilkan hasil visualisasi. Secara default fungsi PCA() akan langsung menampilkan hasil visualisasi

pca_loan <- PCA(loan_clean,
                ncp = 10,
                quali.sup = c(1, 6, 7),
                graph = F)

Setelah membuat PCA, selanjutnya adalah membuat visualisasi dari hasil PCA. Kita akan membuat individual plot menggunakan fungsi fviz_pca_ind() dari library factoextra. Parameter yang digunakan adalah:

• Objek hasil PCA
• habillage: Nomor kolom dari variabel kategorik, setiap individu akan dibedakan berdasarkan variabel kategori yang dipilih
• select.ind: Jumlah individu dengan kontribusi tertinggi yang ingin dilihat

fviz_pca_ind(pca_loan,
             habillage = 6,
             select.ind = list(contrib = 10))

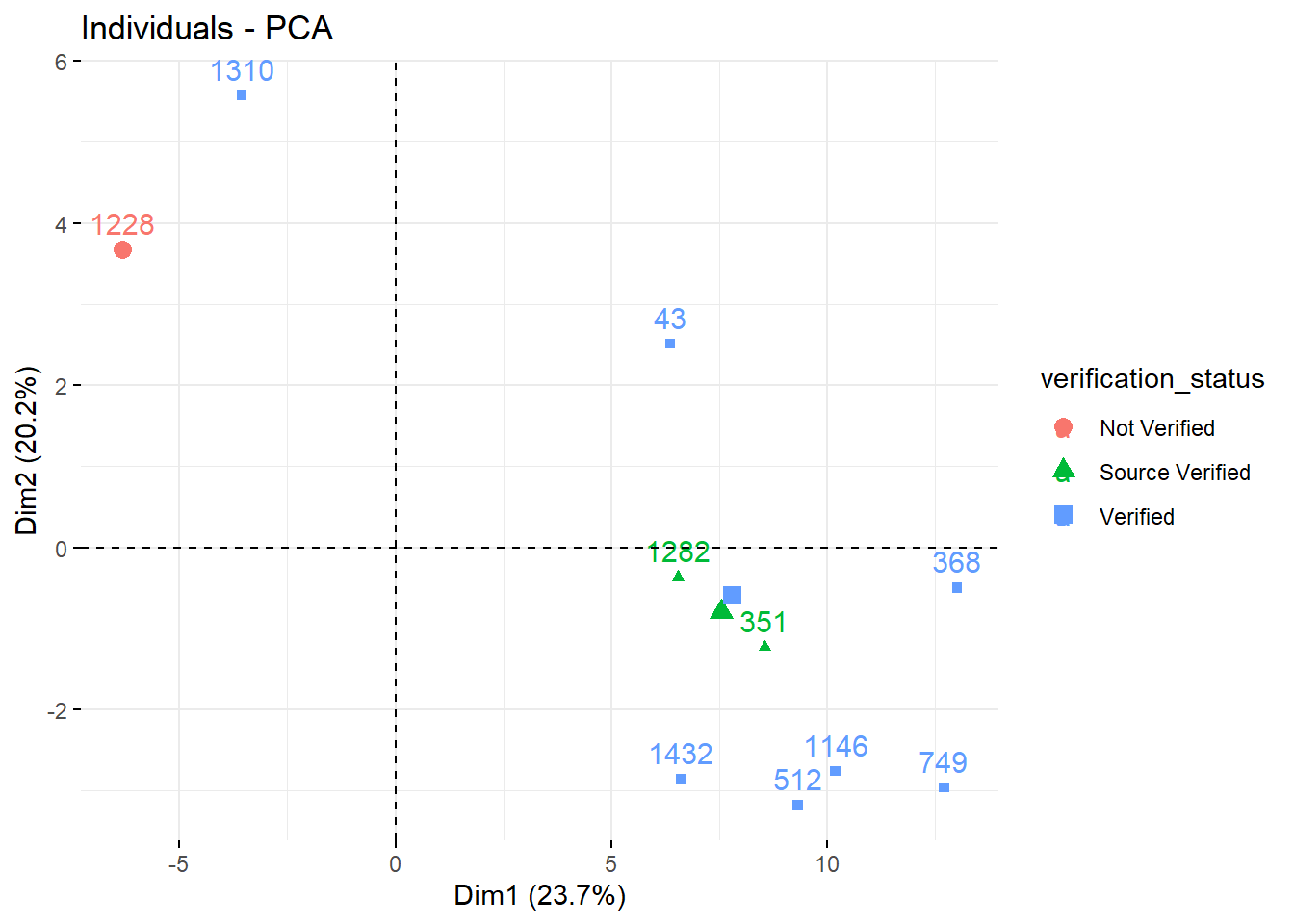
Plot individu di atas hanya menampilkan 10 observasi yang memberikan informasi tertinggi terhadap PC1 dan PC2. Namun, terdapat lebih dari 10 titik observasi yang terdapat pada plot di atas karena terdapat titik observasi yang merupakan titik pusat dari tiap status verifikasi.

7.2.4 Bagaimana cara PCA menentukan outlier dari individual plot dan langsung ekstrak daftar outlier menjadi sebuah vector?

Misalkan kita menggunakan individual plot dari pca_loan untuk melihat 5 observasi yang tergolong outlier, sebagai berikut:

plot.PCA(pca_loan, choix = "ind", select = "contrib 5")

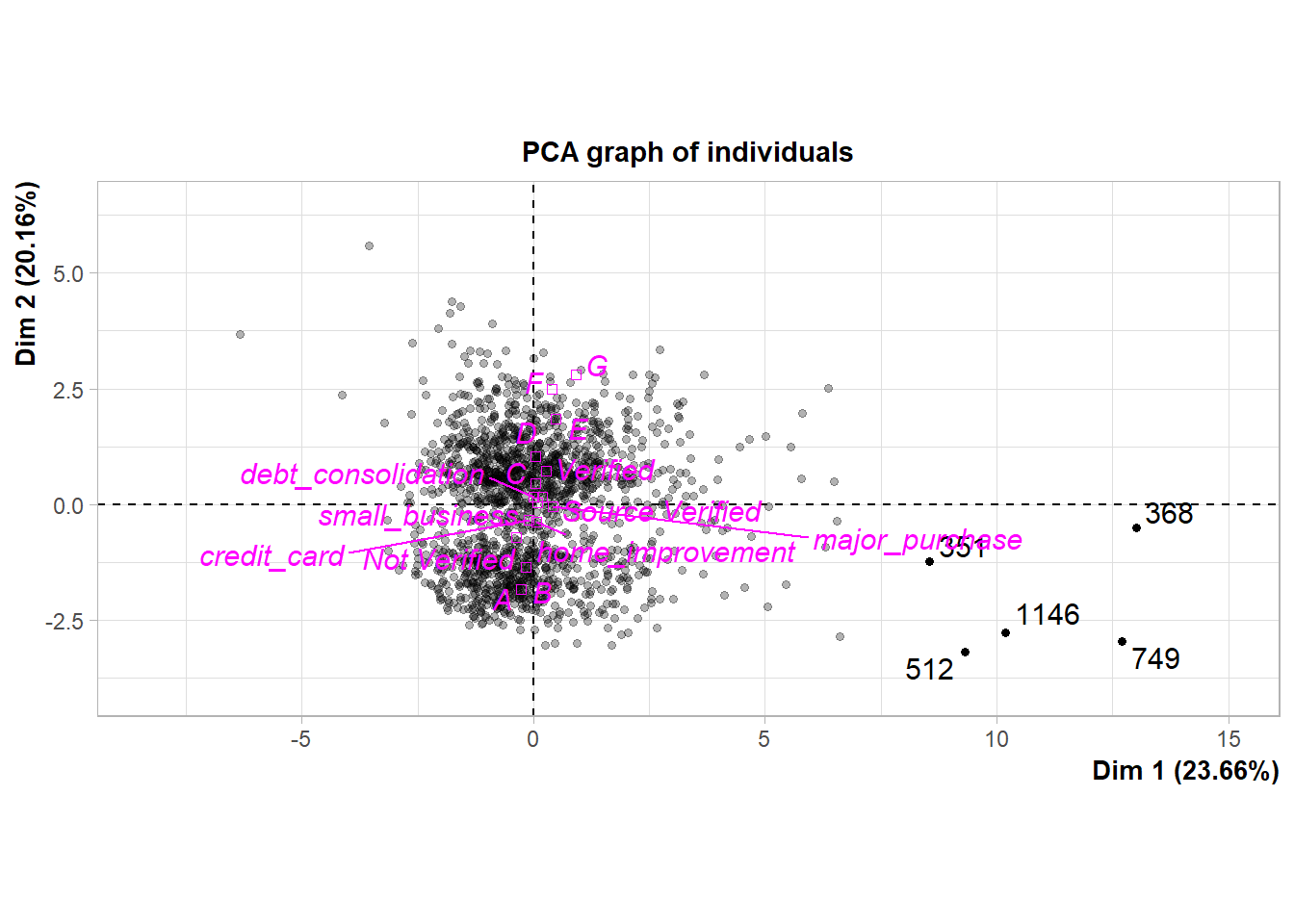
Tujuan kita adalah untuk mengekstrak label outlier yang ditampilkan pada individual plot di atas. Berdasarkan dokumentasi fungsi plot.PCA(), outlier ditentukan melalui jumlah kuadrat koordinat (Sum of Squares SS) tertinggi dari dimensi yang dipilih pada individual plot. Secara default, PC yang digunakan adalah PC1 (Dim.1) dan PC2 (Dim.2).

coord_mat <- pca_loan$ind$coord
data.frame("outlier_name" = row.names(coord_mat),
           coord_mat) %>% 
  mutate(SS = Dim.1^2 + Dim.2^2) %>% # sesuaikan dengan PC yang dipilih
  arrange(-SS) %>% 
  head(5) %>% # sesuaikan dengan jumlah outlier yang diambil
  pull(outlier_name)

#> [1] "749"  "368"  "1146" "512"  "351"

7.3 Clustering

7.3.1 Bagaimana best practice dalam penentuan jumlah cluster?

Fungsi kmeans() tidak dapat menentukan jumlah cluster secara otomatis. Jumlah cluster tetap ditentukan oleh user berdasarkan kebutuhan bisnis. Namun, secara statistik penentuan jumlah cluster dapat dilakukan berdasarkan penurunan Within Sum of Square (WSS). Secara sederhana, penurunan WSS dapat divisualisasikan dengan menggunakan fungsi fviz_nbclust() dari library factoextra. Berikut contoh memvisualisasikan penurunan WSS dengan menggunakan data USArrests:

head(USArrests, 6)

#>            Murder Assault UrbanPop Rape
#> Alabama      13.2     236       58 21.2
#> Alaska       10.0     263       48 44.5
#> Arizona       8.1     294       80 31.0
#> Arkansas      8.8     190       50 19.5
#> California    9.0     276       91 40.6
#> Colorado      7.9     204       78 38.7

# scaling data
USArrests_scale <- scale(USArrests)

Melakukan visualisasi penurunan WSS dengan menggunakan fungsi fviz_nbclust() dari library factoextra.

set.seed(100)
fviz_nbclust(USArrests_scale, method = "wss", kmeans)

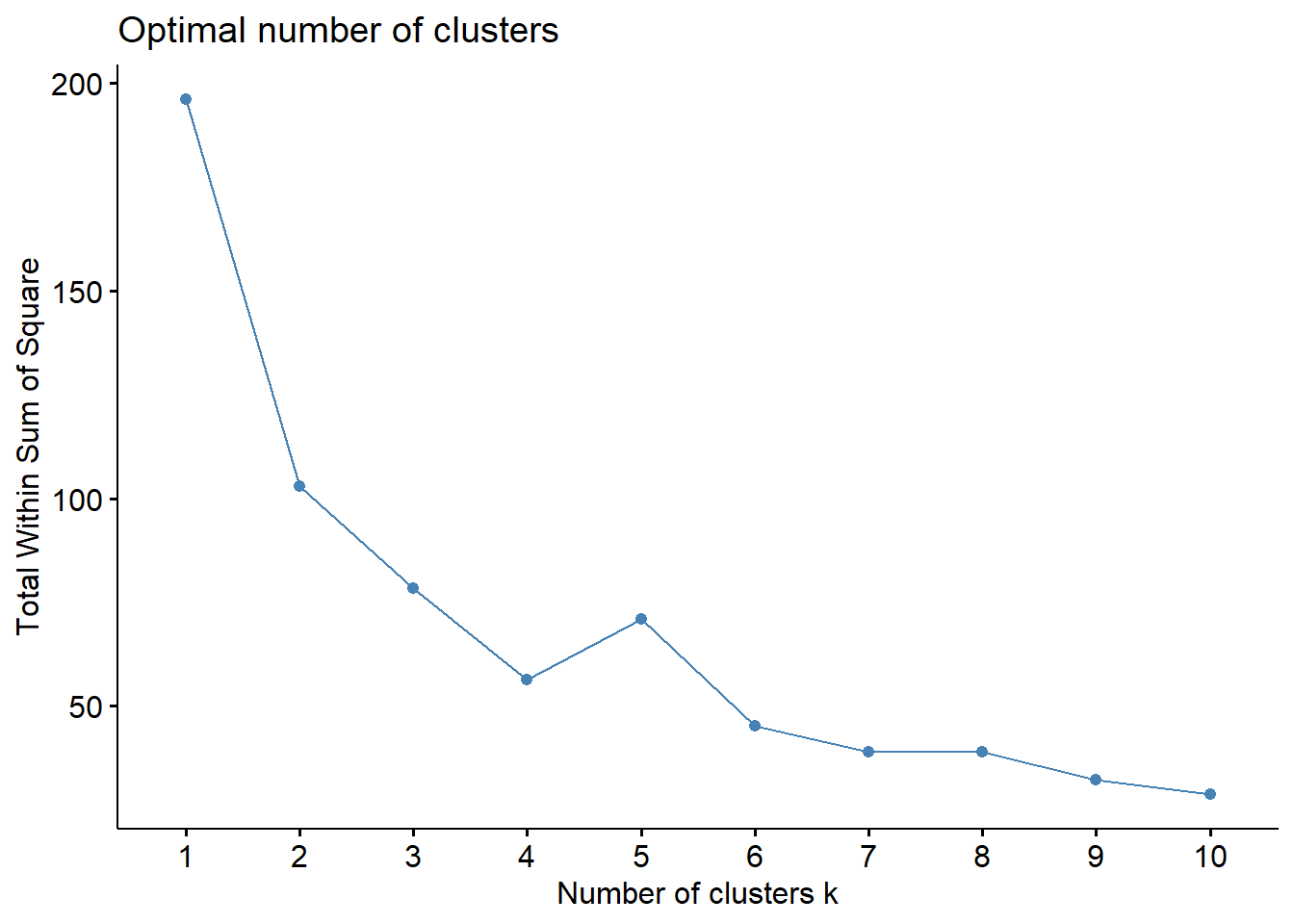
Jumlah cluster yang dipilih adalah jumlah cluster yang ketika dilakukan penambahan cluster sudah tidak mengakibatkan penurunan WSS yang signifikan (pada grafik bentuknya landai), kemudian disesuaikan dengan kebutuhan bisnis pada industri.

7.3.2 Bagaimana implementasi visualisasi K-means clustering menggunakan package factoextra?

Kita akan mencoba melakukan visualisasi hasil clustering dengan menggunakan data USArrests.

head(USArrests, 5)

#>            Murder Assault UrbanPop Rape
#> Alabama      13.2     236       58 21.2
#> Alaska       10.0     263       48 44.5
#> Arizona       8.1     294       80 31.0
#> Arkansas      8.8     190       50 19.5
#> California    9.0     276       91 40.6

# scaling data `USArrests`
USArrests_scale <- scale(USArrests)

Menentukan jumlah cluster yang akan dibuat berdasarkan penurunan WSS, dengan menggunakan fungsi fviz_nbclust() dari library factoextra.

set.seed(100)
fviz_nbclust(USArrests_scale, method = "wss", kmeans)

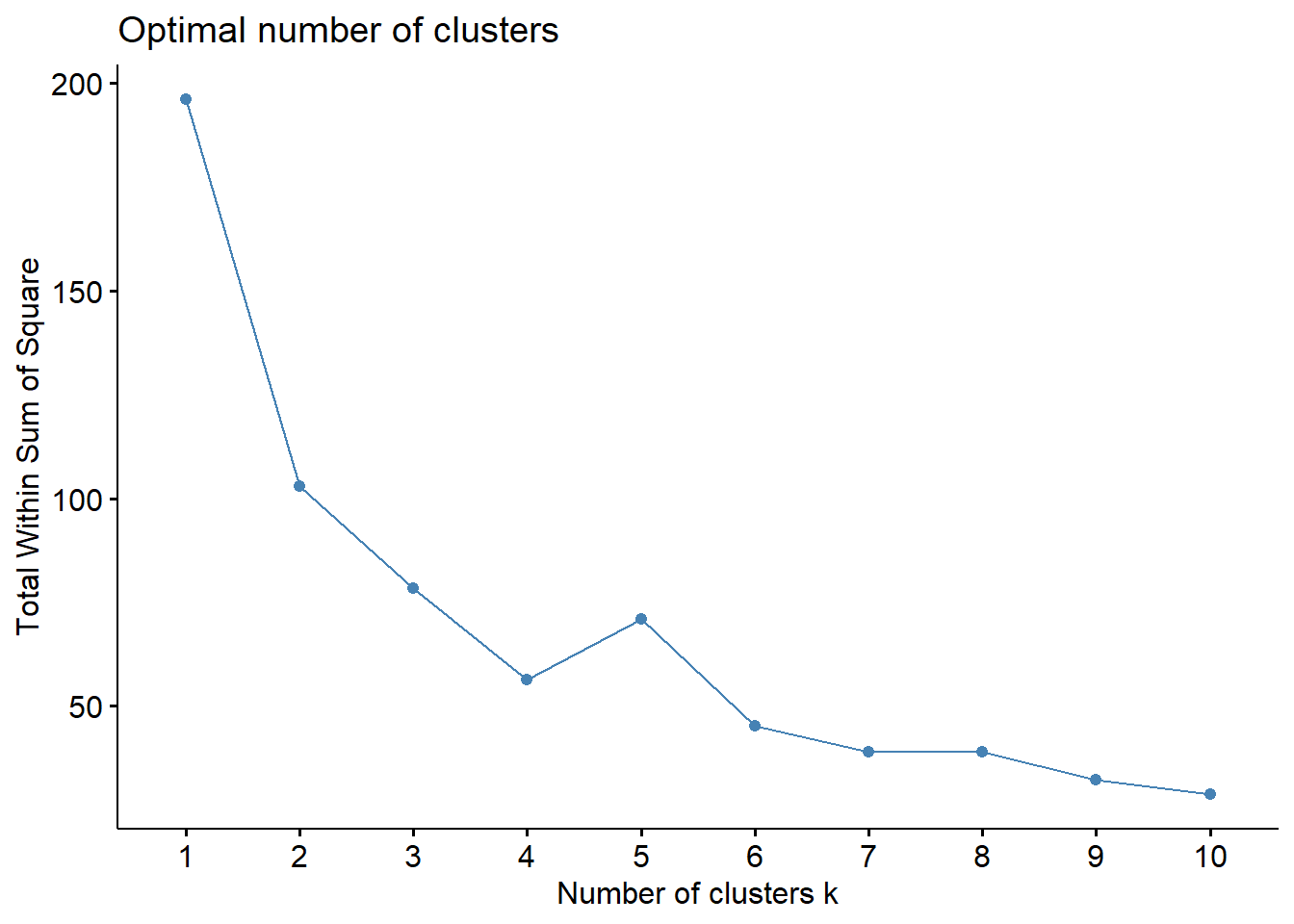
Melakukan k-means clustering dengan jumlah cluster 5 berdasarkan hasil penurunan wss di atas menggunakan fungsi kmeans().

set.seed(100)
USArrests_cl <- kmeans(USArrests_scale, centers = 5)

Membuat visualisasi hasil cluster dengan menggunakan fungsi fviz_cluster() dari library factoextra.

# `USArrests` bisa diganti dengan yang sudah dilakukan scaling `USArrests_scale` 
fviz_cluster(USArrests_cl, USArrests)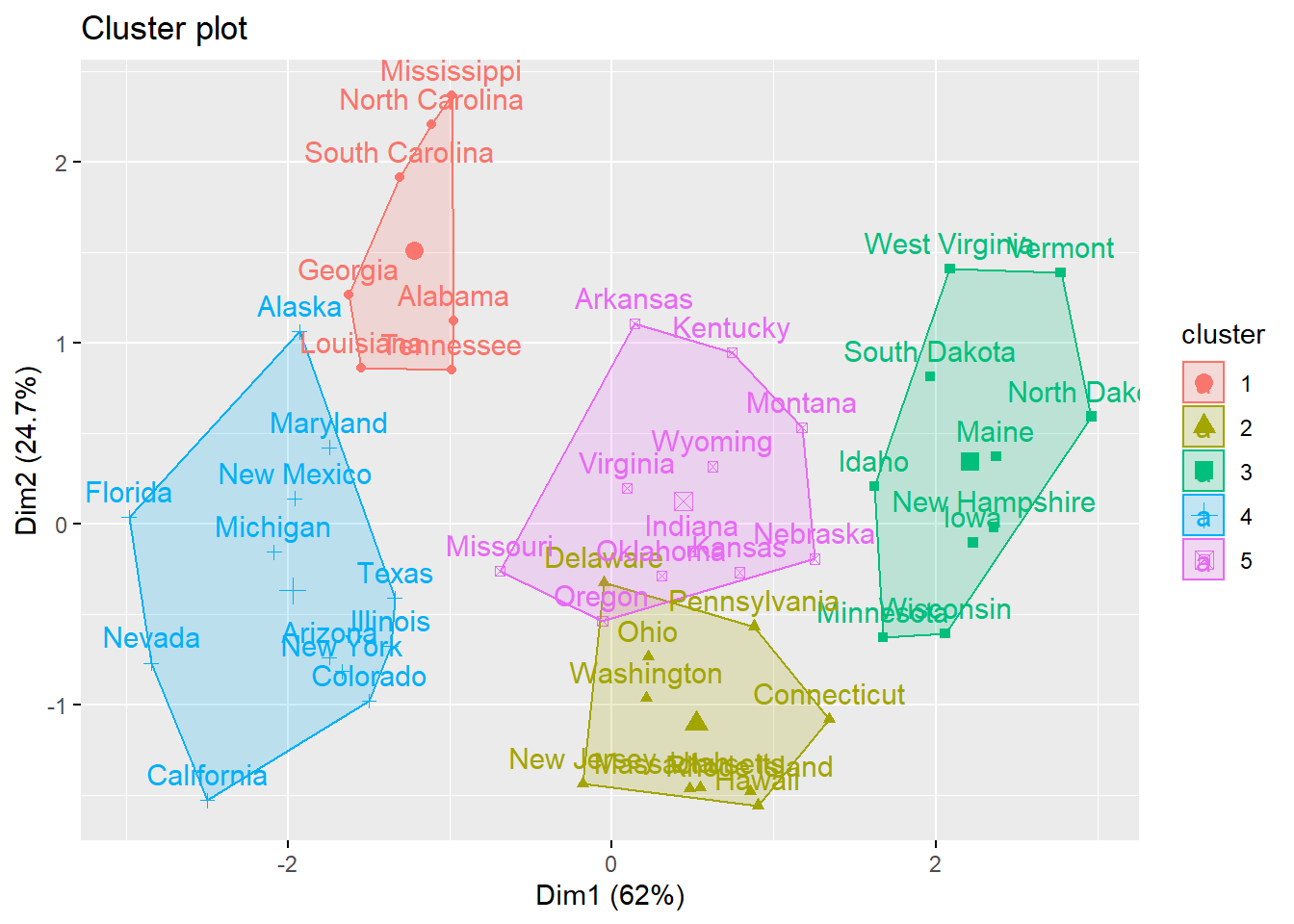

Mengkombinasikan visualisasi hasil clustering dengan PCA. Untuk melakukan hal tersebut kita harus menambahkan kolom cluster pada data USArrests.

USArrests_clean <- USArrests %>% 
  mutate(cluster = USArrests_cl$cluster)

head(USArrests_clean, 5)

#>            Murder Assault UrbanPop Rape cluster
#> Alabama      13.2     236       58 21.2       1
#> Alaska       10.0     263       48 44.5       4
#> Arizona       8.1     294       80 31.0       4
#> Arkansas      8.8     190       50 19.5       5
#> California    9.0     276       91 40.6       4

Mengubah nama baris yang awalnya berupa indeks menjadi nama negara sesuai dengan data USArrests.

rownames(USArrests_clean) <- rownames(USArrests)
head(USArrests_clean, 5)

#>            Murder Assault UrbanPop Rape cluster
#> Alabama      13.2     236       58 21.2       1
#> Alaska       10.0     263       48 44.5       4
#> Arizona       8.1     294       80 31.0       4
#> Arkansas      8.8     190       50 19.5       5
#> California    9.0     276       91 40.6       4

Membuat PCA terlebih dahulu untuk mengkombinasikan visualisasi hasil clustering dengan PCA dengan menggunakan PCA().

pca_USArrest <- PCA(USArrests_clean, quali.sup = 5, graph = F)

Mengkombinasikan visualisasi hasil clustering dan PCA menggunakan fungsi fviz_pca_biplot() dari library factoextra. Parameter yang digunakan adalah:

• Objek hasil PCA
• habillage: Nomor kolom dari variabel kategorik, setiap individu akan dibedakan berdasarkan variabel kategori yang dipilih.
• addEllipses: Sebuah logical value. T akan menambah elips untuk ssetiap cluster, F sebaliknya. Secara default fungsi fviz_pca_biplot() tidak akan menambah elips pada plot individu.

fviz_pca_biplot(pca_USArrest, habillage = 5, addEllipses = T)

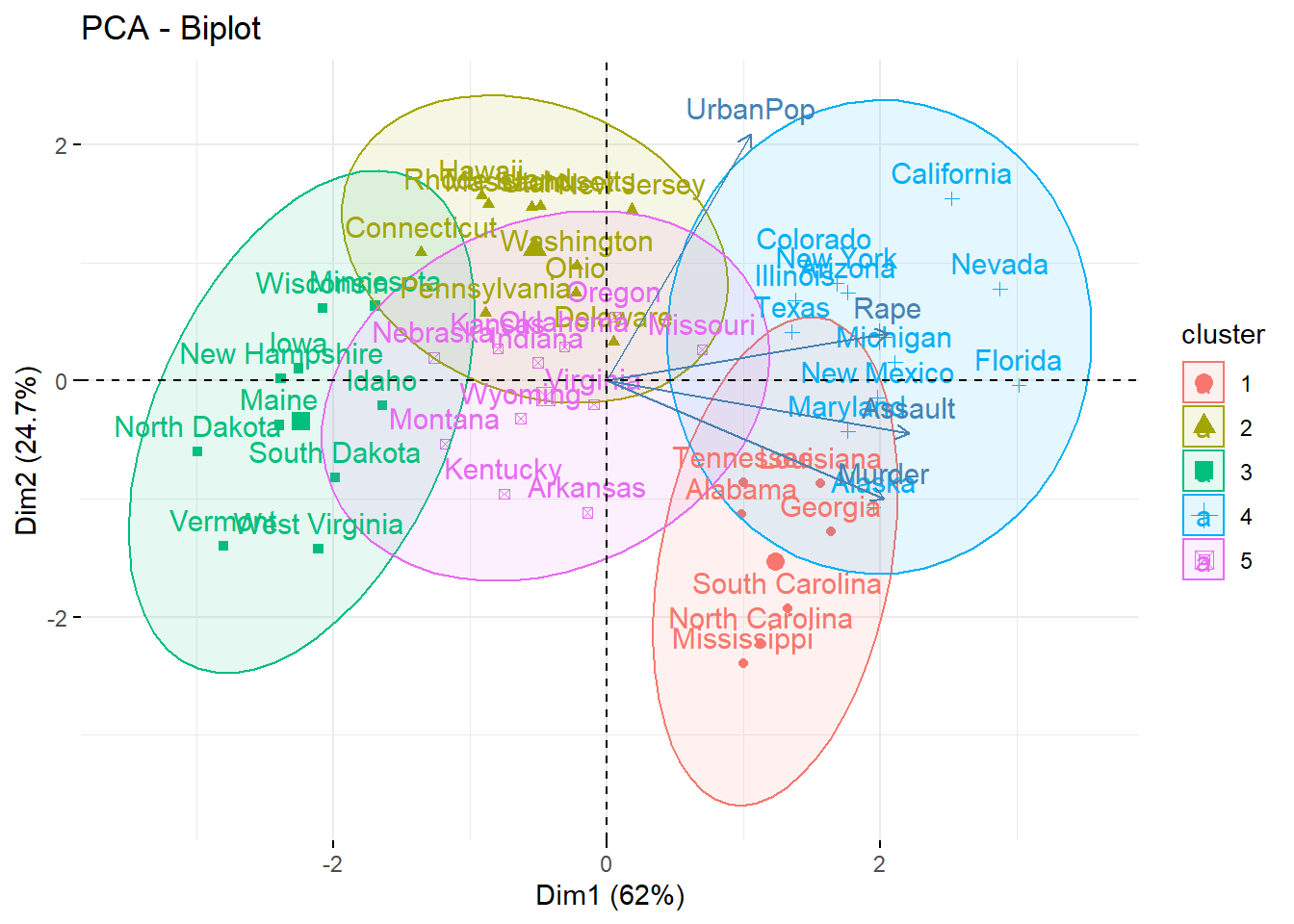
Dari plot di atas terlihat bahwa antar cluster saling tumpang tindih, namun kenyataannya antar cluster pasti memiliki observasi/individu yang unik. Hal tersebut terjadi karena kita mencoba untuk memvisualisasikan cluster yang dibentuk dari 4 dimensi menjadi 2 dimensi saja.

7.3.3 Bagaimana memberikan penamaan label dari hasil clustering?

Algoritma clustering hanya memberikan label 1 sampai $k$, di mana $k$ adalah banyaknya cluster yang terbentuk. Untuk melakukan cluster profiling atau pemberian nama cluster harus berdasarkan hasil interpretasi manusia. Alat bantu cluster profiling yang dapat digunakan adalah:

• Melalui visualisasi PCA - biplot menggunakan fviz_pca_biplot()
• Melihat rangkuman nilai rata-rata (centroid) untuk masing-masing cluster

Sebagai contoh, dari hasil sebelumnya, didapatkan 5 clusters untuk mengelompokkan negara bagian US berdasarkan tingkat kriminalitas dan besar populasinya. Berikut interpretasi clusternya:

USArrests_clean %>% 
  group_by(cluster) %>% 
  summarize_all(mean)

#> # A tibble: 5 x 5
#>   cluster Murder Assault UrbanPop  Rape
#>     <int>  <dbl>   <dbl>    <dbl> <dbl>
#> 1       1  14.7    251.      54.3  21.7
#> 2       2   5.05   137.      79.3  17.6
#> 3       3   2.68    70.1     51    10.9
#> 4       4  11.0    264       76.5  33.6
#> 5       5   7.07   140.      61.5  20.1

• Cluster 1: HIGH crime rate, but MODERATE population -> “HIGH-MODERATE”
• Cluster 2: LOW crime rate, but HIGH population -> “LOW-HIGH”
• Cluster 3: LOWEST crime rate and population -> “LOWEST”
• Cluster 4: HIGHEST crime rate and population -> “HIGHEST”
• Cluster 5: MODERATE crime rate and population -> “MODERATE”

Menyiapkan dataframe berisi pemetaan dari nomor cluster menjadi label yang diinginkan:

mapping_label <- data.frame(cluster = 1:5,
                            label = c("HIGH-MODERATE", "LOW-HIGH", 
                                      "LOWEST", "HIGHEST",
                                      "MODERATE"))

mapping_label

#>   cluster         label
#> 1       1 HIGH-MODERATE
#> 2       2      LOW-HIGH
#> 3       3        LOWEST
#> 4       4       HIGHEST
#> 5       5      MODERATE

Melakukan join table USArrests_clean dan mapping_label dengan fungsi join() dari library plyr:

USArrests_clean %>% 
  rownames_to_column("State") %>% 
  plyr::join(mapping_label) %>% 
  select(State, label)

#>             State         label
#> 1         Alabama HIGH-MODERATE
#> 2          Alaska       HIGHEST
#> 3         Arizona       HIGHEST
#> 4        Arkansas      MODERATE
#> 5      California       HIGHEST
#> 6        Colorado       HIGHEST
#> 7     Connecticut      LOW-HIGH
#> 8        Delaware      LOW-HIGH
#> 9         Florida       HIGHEST
#> 10        Georgia HIGH-MODERATE
#> 11         Hawaii      LOW-HIGH
#> 12          Idaho        LOWEST
#> 13       Illinois       HIGHEST
#> 14        Indiana      MODERATE
#> 15           Iowa        LOWEST
#> 16         Kansas      MODERATE
#> 17       Kentucky      MODERATE
#> 18      Louisiana HIGH-MODERATE
#> 19          Maine        LOWEST
#> 20       Maryland       HIGHEST
#> 21  Massachusetts      LOW-HIGH
#> 22       Michigan       HIGHEST
#> 23      Minnesota        LOWEST
#> 24    Mississippi HIGH-MODERATE
#> 25       Missouri      MODERATE
#> 26        Montana      MODERATE
#> 27       Nebraska      MODERATE
#> 28         Nevada       HIGHEST
#> 29  New Hampshire        LOWEST
#> 30     New Jersey      LOW-HIGH
#> 31     New Mexico       HIGHEST
#> 32       New York       HIGHEST
#> 33 North Carolina HIGH-MODERATE
#> 34   North Dakota        LOWEST
#> 35           Ohio      LOW-HIGH
#> 36       Oklahoma      MODERATE
#> 37         Oregon      MODERATE
#> 38   Pennsylvania      LOW-HIGH
#> 39   Rhode Island      LOW-HIGH
#> 40 South Carolina HIGH-MODERATE
#> 41   South Dakota        LOWEST
#> 42      Tennessee HIGH-MODERATE
#> 43          Texas       HIGHEST
#> 44           Utah      LOW-HIGH
#> 45        Vermont        LOWEST
#> 46       Virginia      MODERATE
#> 47     Washington      LOW-HIGH
#> 48  West Virginia        LOWEST
#> 49      Wisconsin        LOWEST
#> 50        Wyoming      MODERATE

7.4 Mathematics Concept

7.4.1 Principal Component Analysis

1. Tujuan: membuat axis baru yang dapat merangkum informasi data

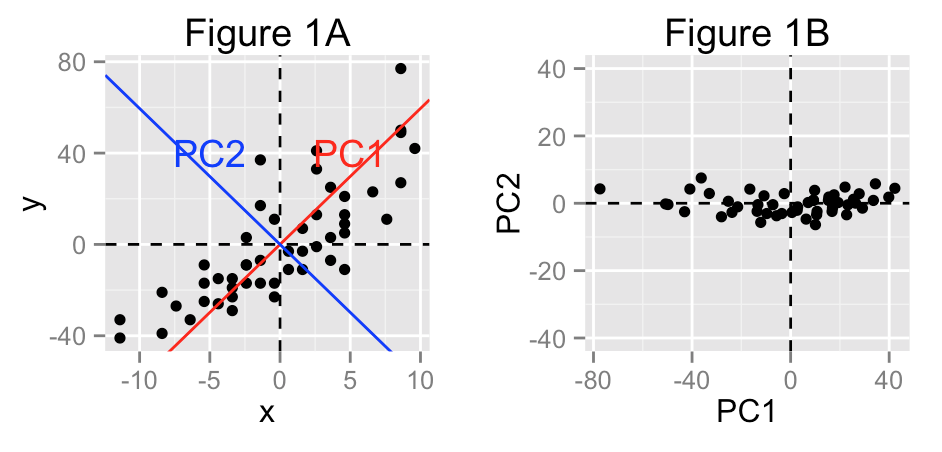
Kita akan menggunakan data dummy yang disimpan pada objek A, yang terdiri dari variabel x dan y.

set.seed(100)
x <- runif(200)
A <- data.frame(x=x, y=-x+runif(100, 1.05, 1.25))
head(A)

#>            x         y
#> 1 0.30776611 0.8161531
#> 2 0.25767250 0.9835921
#> 3 0.55232243 0.6803929
#> 4 0.05638315 1.1582841
#> 5 0.46854928 0.6453471
#> 6 0.48377074 0.7417693

Sebelum menghitung matriks variance-covariance harus dilakukan scaling terlebih dahulu, karena nilai variance dan covariance sangat bergantung pada interval nilai dari data.

A <- scale(A, center = T)
head(A)

#>                x             y
#> [1,] -0.69524199  0.5781964712
#> [2,] -0.87017881  1.1453429992
#> [3,]  0.15879719  0.1183517145
#> [4,] -1.57312115  1.7370570727
#> [5,] -0.13375526 -0.0003546811
#> [6,] -0.08059893  0.3262449661

Membuat visualisasi data yang disimpan pada objek A.

plot(A, cex=0.4)

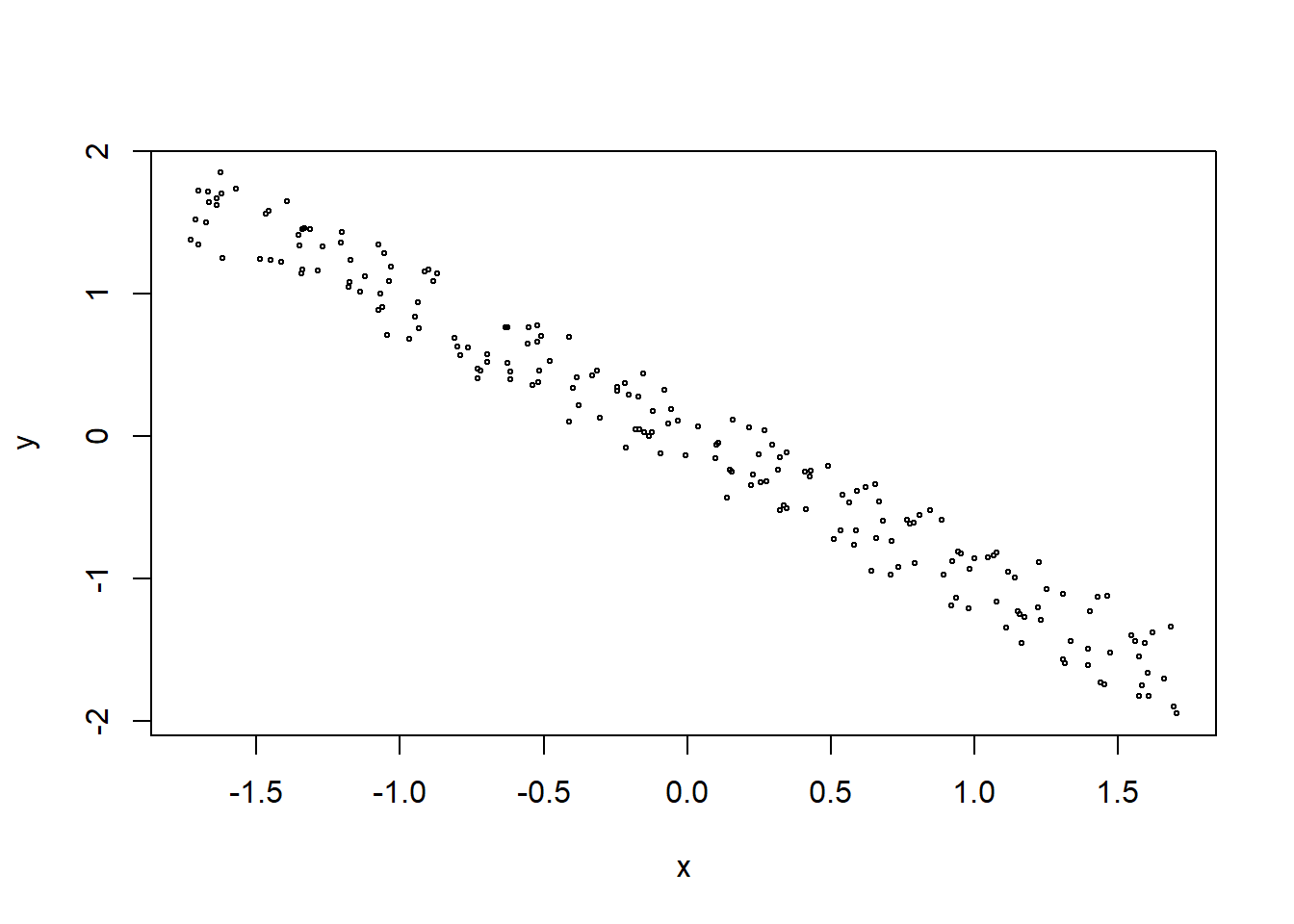
Variabel x dan y berkorelasi secara negatif, karena variabel y dibentuk dari operasi matematika dari variabel x (dengan kata lain variabel y mengandung informasi dari x).

2. PC merangkum informasi dari actual data sehingga akan dihitung variance-covariance (variance-covariance merepresentasikan informasi yang terkandung pada suatu data)

var(A)

#>           x         y
#> x  1.000000 -0.982719
#> y -0.982719  1.000000

class(var(A))

#> [1] "matrix" "array"

# alternatif: menggunakan `cov()` untuk menghitung variance-covariance
# cov(A)
# cor(A)

Jika diperhatikan variance-covariance yang dihasilkan berupa matriks, dalam aljabar terdapat beberapa operasi perkalian untuk kelas matriks:

• Perkalian vektor dengan skalar (konstanta)

matrix(c(2,3)) %*% 2

#>      [,1]
#> [1,]    4
#> [2,]    6

Membuat plot untuk melihat vektor awal

plot(2, 3)
lines(x = c(0, 2), y = c(0, 3))

Membuat plot untuk membandingkan vektor awal dan setelah dilakukan operasi perkalian dengan skalar (konstanta)

plot(x = c(2, 4), y = c(3, 6))
lines(x = c(0, 4), y = c(0, 6))

Operasi perkalian antara vektor dengan skalar (konstanta) akan memperbesar vektor dengan arah yang sama.

• Perkalian matriks dengan vektor

matrix(1:4, nrow = 2) %*% matrix(c(2, 3))

#>      [,1]
#> [1,]   11
#> [2,]   16

Membuat plot untuk membandingkan vektor awal dan setelah dilakukan operasi perkalian dengan matriks

plot(x = c(2, 11), y = c(3, 16))
lines(x = c(0, 2), y = c(0, 3))
lines(x = c(0, 11), y = c(0, 16))

Jika diperhatikan kedua vektor tersebut seperti berada dalam satu garis karena hampir sejajar, namun jika dicek nilai slope ($y/x$) akan sangat jelas berbeda.

# vektor awal
3/2

#> [1] 1.5

# vektor setelah dilakukan operasi perkalian dengan matriks
16/11

#> [1] 1.454545

Operasi perkalian antara matriks dengan vektor akan mengubah besar dan arah vektor

• Perkalian matriks identitas dengan vektor

matrix(c(1, 0, 0, 1), nrow = 2) %*% matrix(c(2, 3))

#>      [,1]
#> [1,]    2
#> [2,]    3

Operasi perkalian antara matriks dengan vektor akan mengubah besar dan arah vektor, namun terdapat matriks yang jika dikalikan dengan vektor tidak akan mengubah besar dan arah vektor, yaitu matriks identitas.

• Perkalian matriks rotasi dengan vektor

matrix(c(-1, 0, 0, -1), nrow = 2) %*% matrix(c(-3, 2))

#>      [,1]
#> [1,]    3
#> [2,]   -2

Membuat plot untuk melihat vektor awal

plot(-3, 2)
lines(x = c(0, -3), y = c(0, 2))

Membuat plot untuk membandingkan vektor awal dan setelah dilakukan operasi perkalian dengan matriks rotasi

plot(3, -2)
lines(x = c(0, 3), y = c(0, -2))

Operasi perkalian antara matriks dengan vektor akan mengubah besar dan arah vektor, namun terdapat matriks yang jika dikalikan dengan vektor hanya akan mengubah arah vektor, yaitu matriks rotasi.

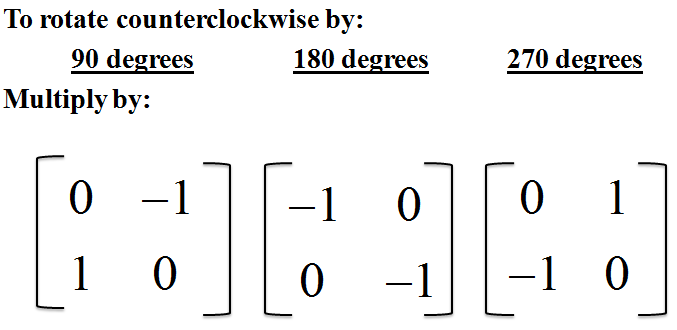
• Perkalian matriks dengan eigen vektor

Operasi perkalian antara matriks dengan vektor akan mengubah besar dan arah vektor. Namun, terdapat vektor yang unik yang jika dikalikan dengan matriks hasilnya sama dengan mengalikan vektor dengan skalar.

Skalar tersebut adalah konstanta yang disebut sebagai eigen value. Ketika kita mengalikan matriks A dengan eigen vector $x$, hasilnya adalah konstanta $\lambda$ dikalikan $x$. Maka persamaannya adalah:

$$Ax=\lambda x$$

• $A$ merupakan matriks variance-covariance
• $x$ merupakan eigen vector
• $\lambda$ merupkan skalar (konstanta) yang disebut eigen value.

Eigen vektor tersebut digunakan sebagai transformasi untuk mengubah arah/menentukan arah axis baru yang lebih bisa merangkum informasi pada actual data.

3. Variance-covariance yang memuat informasi pada actual data akan digunakan untuk memperoleh eigen vektor (transformasi) dan eigen value.

eigen(var(A))

#> eigen() decomposition
#> $values
#> [1] 1.98271899 0.01728101
#> 
#> $vectors
#>            [,1]       [,2]
#> [1,] -0.7071068 -0.7071068
#> [2,]  0.7071068 -0.7071068

Eigen value memuat jumlah informasi yang dirangkum oleh setiap PC, sehingga total eigen value akan sama dengan jumlah variabel pada actual data.

1.98271899 + 0.01728101

#> [1] 2

4. Membuat new data (PC) dari hasil perkalian antara actual data dengan eigen vektor (transformasi).

New data tersebut akan memuat informasi yang sama dengan actual data dengan arah yang berbeda dari actual data.

$$newdata=actualdata\times eigenvektor$$

# dim(200x2) x dim(2x2)
hasil_pc1 <- A %*% eigen(var(A))$vectors

Bab 8 Time Series and Forecasting

8.1 Data Preprocessing

8.1.1 Data time series yang digunakan untuk forecasting harus terurut, lengkap, dan tidak diperbolehkan terdapat missing value (NA). Bagaimana cara melengkapi urutan waktu yang hilang pada data time series?

Misal terdapat dataframe seperti berikut:

Quantity <- c(3,4,5)
Order.Date <- c("2019-01-03","2019-01-07","2019-01-08") 
dat <- data.frame(Order.Date, Quantity) %>% 
       mutate(Order.Date = ymd(Order.Date)) 
dat

#>   Order.Date Quantity
#> 1 2019-01-03        3
#> 2 2019-01-07        4
#> 3 2019-01-08        5

Anda dapat menggunakan fungsi pad() dari package padr untuk melengkapi urutan waktu di atas

library(padr)
dat %>% 
  pad()

#>   Order.Date Quantity
#> 1 2019-01-03        3
#> 2 2019-01-04       NA
#> 3 2019-01-05       NA
#> 4 2019-01-06       NA
#> 5 2019-01-07        4
#> 6 2019-01-08        5

8.1.2 Bagaimana cara melakukan imputasi untuk mengisi nilai NA pada objek time series?

Salah satu cara yang dapat digunakan adalah mengisi nilai NA dengan fungsi na.fill() dari package zoo. Pada fungsi tersebut terdapat parameter fill yang digunakan untuk mendefiniskan algoritma yang digunakan untuk mengisis nilai NA, salah satunya adalah “extend” (nilai NA pada objek time series akan diisi dengan nilai yang berada di sekitar nilai NA tersebut). Penjelasan lebih detail mengenai fungsi na.fill() dapat dilihat pada dokumentasi berikut Prophet&AnomalyDetection

library(zoo)
dat %>% 
  pad() %>% 
  pull(Quantity)  %>% 
  ts(frequency = 7) %>% 
  na.fill(fill = "extend") 

#> Time Series:
#> Start = c(1, 1) 
#> End = c(1, 6) 
#> Frequency = 7 
#> [1] 3.00 3.25 3.50 3.75 4.00 5.00

Selain menggunakan fungsi di atas, Anda juga dapat menggunakan berbagai fungsi imputasi dari package imputeTS untuk mengisi nilai NA pada objek time series. Time Series Imputation with imputeTS

8.2 Time Series

8.2.1 Apakah yang dimaksud dengan data time series?

Data time series merupakan data yang dikumpulkan berdasarkan interval waktu yang sama. Urutan waktu yang digunakan dapat berupa detik, menit jam, hari, minggu, bulan, dll.

8.2.2 Apa perbedaan analisis time series dan regresi?

Perbedaan utama antara analisis regresi dengan analisis time series adalah prediktor yang digunakan, jika analisis regresi menggunakan faktor exogenous sebagai prediktor. Tidak pada analisis time series yang mengggunakan nilai target di masa lampau sebagai prediktor (lag)

• Analisis regresi: $Y=X_1+X_2+X_3+...+X_n$

• Analisis time series: $Y_{t+1}=Y_t+Y_{t-1}+Y_{t-2}+...+Y_{t-n}$

8.2.3 Bagaimana jika hasil decomposition pada bagian trend masih cenderung membentuk pola berulang (seasonal)?

Hal tersebut berarti masih terdapat pola berulang (seasonal) yang belum terangkum, kemungkinan data time series tersebut tidak hanya memiliki 1 pola berualang (seasonal). Melainkan, memiliki lebih dari 1 pola berulang (multiple seasonal). Anda bisa mencoba membuat objek msts (multiple seasonal time series) dengan menggunakan fungsi msts() dari package forecast, kemudian lakukan kembali decomposition untuk mengonfirmasi apakah periode/frekuensi seasonal yang digunakan sudah tepat atau belum. Penjelasan lebih lengkap mengenai multiple seasonal time series dapat dilihat pada multiple seasonal

8.2.4 Apakah terdapat tes/uji statistik yang dapat digunakan untuk mengetahui ada atau tidaknya pola seasonal pada data time series?

Anda dapat melakukan beberapa cara untuk mengetahui ada tidaknya pola seasonal pada data time series, yaitu:

• Melakukan exploratory data dengan membuat line plot
• Melakukan WO test

Namun, menurut Rob Hyndman tes di atas hanya dapat digunakan sebagai referensi tambahan untuk memperkuat deteksi yang dilakukan dengan menggunakan line plot bukan sebagai tools confirmation. Penjelasan lebih lengkap mengenai pernyataan Rob Hyndman dapat Anda baca pada referensi berikut Detecting seasonality.

• Menghitung seasoanality strength menggunakan fungsi stl_features() dari package tsfeatures. Introduction to the tsfeatures package: stl_featues

8.2.5 Pola seasonal biasanya berulang setiap $k$ periode/frekuensi yang sama, namun bagaimana jika pola seasonal pada data time series berulang pada periode/frekuensi yang berbeda. Misal, hari raya lebaran selalu bergeser setiap tahunnya. Bagaimana menentukan periode/frekuensi seasonal pada data time series tersebut?

Secara umum pola seasonal diambil dari pola data time series pada saat terjadi perulangan. Jika menggunakan tanggal tahun hijriah, maka gunakan periode tahun hijriah, yaitu 354.3. Namun, ketika menggunakan preiode/frekuensi tersebut, maka diasumsikan bahwa seluruh observasi (hari) memiliki pola seasonal sesuai periode/frekuensi tahun hijriah. Padahal seharusnya tidak demikian, sehingga seringkali untuk memodelkan kondisi-kondisi tertentu yang dianggap berpengaruh terhadap hasil forcasting dapat menggunakan komponen “external regressor” atau efek “covariates”. Penjelasan lebih lengkap dapat dilihat pada referensi berikut Vector autoregressions

8.2.6 Berapa minimal jumlah sampel data time series untuk melakukan forecasting?

Minimal jumlah sampel data time series yang diperlukan untuk melakukan forecasting adalah 2 periode, hal ini karena ada atau tidaknya pola berulang (seasonal) baru dapat dilihat pada 1 periode setelahnya. Sementara, jika dilakukan cross validation (splitting data) untuk data train minimal 2 periode karena pemodelan dilakukan pada data train. Sementara, jumlah sampel pada data test minimal 1 observasi. Sehingga, 2 periode plus 1 observasi, namun pada kenyaataannya jarang sekali dilakukan forecasting hanya 1 waktu ke depan. Oleh karena itu, biasanya digenapkan menjadi 1 periode untuk data test dan 2 periode untu data train.

8.2.7 Bagaimana menentukan additive maupun multiplicative di trend dan seasonality?

Penentuan additive maupun multiplicative dilakukan melalui visualisasi menggunakan line plot. Berikut adalah klasifikasi pola time series berdasarkan Pegels:

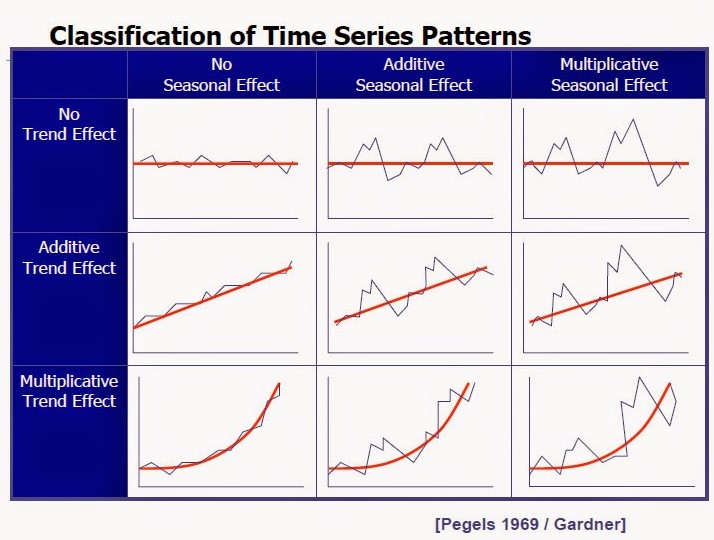
Trend:

• No trend: data time series hanya bergerak di sekitaran rata-rata (konstan membentuk garis lurus horizontal)
• Additive trend: data secara umum bergerak naik/turun secara linear
• Multiplicative trend: data secara umum bergerak naik/turun secara eksponensial

Seasonality:

• No seasonality: tidak ada pola yang berulang pada data (variance cenderung random)
• Additive seasonality: terdapat pola berulang yang cenderung konstan (variance konstan pada setiap periodenya)
• Multiplicative seasonality: terdapat pola berulang yang semakin lama semakin besar/kecil (variance berubah pada setiap periodenya)

8.2.8 Apakah mungkin terdapat data time series multiplicative yang nilainya semakin mengecil?

• Additive: $Y=Trend+Seasonal+Error$

• Multiplicative: $Y=Trend\ast Seasonal\ast Error$

Jika yang dimaksud dengan data time series multiplicative yang nilainya semakin mengecil adalah interval efek seasonality yang semakin mengecil, fenomena tersebut mungkin saja terjadi ketika data time series mengalami trend menurun yang nilainya mempengaruhi interval variansi efek seasonality. Secara matematika hal tersebut mungkin saja terjadi, tetapi jarang sekali terdapat karakteristik data time series yang demikian jika dibandingkan dengan data time series yang memiliki karakteristik interval variansinya semakin membesar.

8.2.9 Apakah fungsi seasonplot() dari pacakage forecast bisa membandingkan tahun-tahun tertentu saja, misalnya membandingkan suatu data time series pada rentang waktu antara tahun 1950 sampai 1951 saja?

Jika langsung menggunakan fungsi tersebut tidak bisa, namun Anda dapat melakukan subsetting pada data time series terlebih dahulu dengan menggunakan fungsi window() seperti berikut

window(AirPassengers, start = 1950, end = 1951) %>% 
  seasonplot(year.labels.left = T)

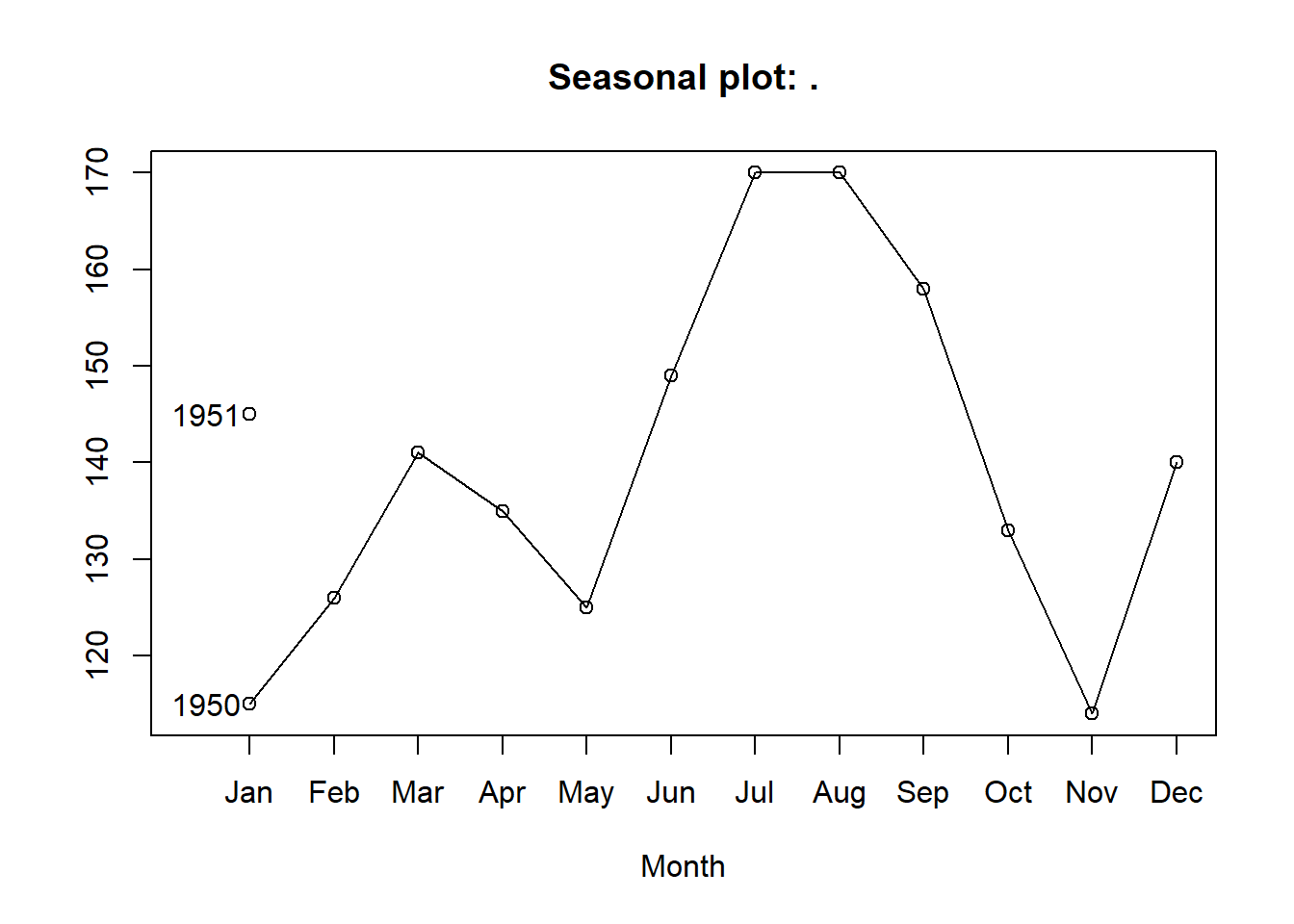
8.3 Forecasting

8.3.1 Apa maksud penggunaan parameter smoothing mendekati 1 pada metode exponential smoothing?

Nilai parameter smoothing 1 berarti memberikan bobot yang lebih besar pada observasi terbaru, sementara observasi yang lebih lama diberikan bobot yang lebih kecil

8.3.2 Apakah pada analisis time series dapat menambahkan prediktor exogenous khususnya pada metode ARIMA?

Anda dapat menambahkan prediktor exogenous pada metode ARIMA dengan menambahkan parameterxreg pada fungsi Arima() dan auto.arima() dari pacakge forecast

library(fpp2)
library(forecast)
Arima(y = uschange[,1], xreg = uschange[,2], order = c(1,1,0))

#> Series: uschange[, 1] 
#> Regression with ARIMA(1,1,0) errors 
#> 
#> Coefficients:
#>           ar1    xreg
#>       -0.5412  0.1835
#> s.e.   0.0638  0.0429
#> 
#> sigma^2 estimated as 0.3982:  log likelihood=-177.46
#> AIC=360.93   AICc=361.06   BIC=370.61

auto.arima(y = uschange[,1], xreg = uschange[,2])

#> Series: uschange[, 1] 
#> Regression with ARIMA(1,0,2) errors 
#> 
#> Coefficients:
#>          ar1      ma1     ma2  intercept    xreg
#>       0.6922  -0.5758  0.1984     0.5990  0.2028
#> s.e.  0.1159   0.1301  0.0756     0.0884  0.0461
#> 
#> sigma^2 estimated as 0.3219:  log likelihood=-156.95
#> AIC=325.91   AICc=326.37   BIC=345.29

Penjelasan lebih lengkap dapat Anda baca pada referensi berikut Regression ARIMA

8.3.3 Apakah hasil forecast dari differencing yang dilakukan secara manual dengan fungsi diff() akan berbeda dengan hasil forecast dari differencing yang dilakukan secara otomatis pada fungsi Arima() atau auto.arima()?

Ya akan berbeda karena perhitungan yang digunakan saat melakukan differencing pada fungsi Arima() ataupun auto.arima() berbeda dengan perhitungan yang digunakan saat melakukan differencing secara manual dengan fungsi diff(). Penjelasan lebih lengkap mengenai perhitungan tersebut dapat Anda baca pada referensi berikut Difference time series before Arima or within Arima

8.3.4 Apakah terdapat semacam referensi (rule of thumb) untuk menentukan nilai alpha, beta, dan gamma pada exponential smoothing?

Tidak ada referensi (rule-of-thumb) mutlak untuk menentukan nilai alpha, beta, dan gamma. Penentuannya bergantung pada sudut pandang bisnis dan permasalahan yang dianalisa. Apabila data terbaru harus diberikan bobot lebih besar, maka Anda dapat menggunakan nilai alpha, beta, dan gamma mendekati satu. Sebaliknya, apabila data terbaru dan data yang lebih lama akan diberikan bobot yang nilainya tidak jauh berbeda, maka Anda dapat menggunakan nilai alpha, beta dan gamma mendekati nol. Ada baikanya sebagai user dapat mencoba beberapa nilai alpha, beta, dan gamma (melakukan hyperparameter tuning) dengan grid search (mencoba berbagai kombinasi alpha, beta dan gamma). Penjelasan lebih lengkap dapat Anda baca pada referensi berikut Tuning Time Series Forecasting Models

8.3.5 Apakah mungkin nilai MAPE hasil forecasting data test untuk model double exponential smoothing (Holt) lebih kecil dibandingkan triple exponential smoothing (Holt Winters)?

Memungkinkan karena penggunaan metode simple exonential smoothing, double exponential smoothing (Holt), ataupun triple exponential smoothing (Holt Winters) bergantung pada ada tidaknya komponen trend dan seasonal pada data time series. Nilai MAPE hasil forecasting data test untuk model double exponential smoothing (Holt) mungkin lebih kecil dibandingkan nilai MAPE hasil forecasting data test untuk model triple exponential smoothing (Holt Winters) ketika data time series hanya mempunyai komponen error dan trend saja. Dimana memang model double exponential smoothng (Holt) lebih cocok digunakan pada kondisi tersebut.

8.4 Evaluation and Assumption

8.4.1 Apa perbedaan MAE, RMSE, dan MAPE?

• MAE (Mean Absolute Error) cocok digunakan ketika data historis memuat nilai outlier karena nilai MAE tidak sensitif terhadap outlier.

• RMSE (Root Mean Square Error) kurang cocok digunakan ketika data historis memuat nilai outlier karena nilai RMSE sangat sensitif terhadap outlier. Namun, lebih jelas dalam menentukan nilai error (relatif kecil atau besar) karena nilai RMSE akan semakin kecil jika error yang dihasilkan kecil dan sebaliknya.

• MAPE (Mean Absolute Percentage Error), MAPE menunjukan rata-rata error absolut hasil forecasting dalam bentuk persentase terhadap data aktual. Namun, MAPE tidak dapat digunakan pada data historis yang memiliki nilai 0.

8.5 Mathematics Formula

Selain mengamati pola trend atau seasonal pada data time series, perlu diperhatikan pula apakah data time series yang dianalisis merupakan model additive atau multiplicative.

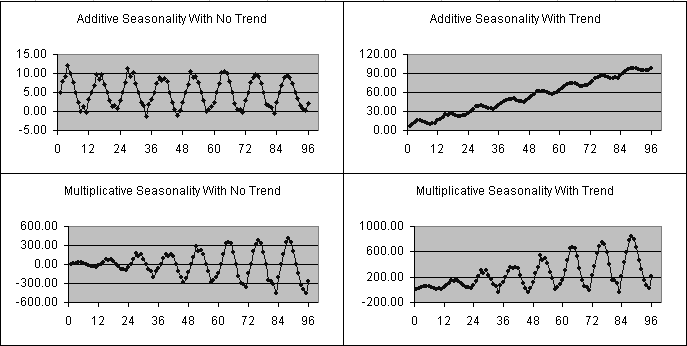
• Additive:

$$Data=Trend+Seasonality+Error$$

• Multiplicative:

$$Data=Trend\ast Seasonality\ast Error$$

Decomposition merupakan metode yang cukup sederhana dan sering digunakan untuk memahami lebih lanjut pola/struktur data time series. Decomposition adalah proses membagi data time series menjadi 3 komponen utama, yaitu:

• trend: pola kenaikan/penurunan
• seasonality: pola berulang
• error: pola yang tidak tertangkap oleh trend dan seasonal

Hasil decomposition digunakan untuk mengecek apakah frequency yang ditentukan saat membuat ojek time series sudah tepat atau belum. Perhatikan pola trend, jika masih belum smooth (membentuk pola selain pola naik/turun) maka frequency yang ditentukan belum tepat. Hal ini terjadi karena masih terdapat pola seasonal yang belum tertangkap.

1. Menghitung secara manual decompose additive model

Import Data

births <- read.csv("data/07-TS/nybirth.csv")

Membuat time series object

births_ts <- ts(data = births$births, start = c(1946, 1), frequency = 12)

Gunakan function decompose()

births_dc <- decompose(x = births_ts, type = "additive")

Objek time series di atas merupakan objek time series dengan model additive, dimana $Data=Trend+Seasonality+Error$

TREND

Trend diperoleh dari hasil pemulusan/smoothing center moving average. Smoothing dilakukan untuk memperoleh pola objek time series yang cenderung naik/turun (trend).

Mengambil nilai trend dari hasil decompose:

births_dc$trend %>% autoplot()

Lakukan smoothing pada data actual untuk memperoleh pola trend dengan metode moving average:

births_trend <- ma(births_ts, order = 12, centre = T)

births_trend %>% autoplot()

SEASONALITY

Mengambil nilai seasonal dari hasil decompose:

births_dc$seasonal %>% autoplot()

Berikut ini merupakan step by step untuk memperoleh nilai seasonal secara manual:

1. Nilai seasonal + nilai error diperoleh dari pengurangan data actual dengan data trend

sea.err_births <- births_ts - births_trend

2. Mencari nilai rata-rata untuk setiap frekuensi

mean.mon_births <- sea.err_births %>% 
  matrix(ncol = 12, byrow = T) %>% 
  colMeans(na.rm = T)

3. Mencari nilai rata-rata global data time series

mean.glo_births <- mean(mean.mon_births)

4. Mencari selisih dari rata-rata untuk setiap frekuensi dengan rata-rata global

mean.mon_births - mean.glo_births

#>  [1] -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556
#>  [7]  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197

5. Setelah diperoleh nilai seasonal dapat diimplementasikan untuk setiap frekuensi

births_seasonal <- ts(rep(mean.mon_births - mean.glo_births, 14), start = start(births_ts), frequency = 12)

births_seasonal %>% autoplot()

ERROR

$Error=Data-Trend-Seasonality$

Mengambil nilai error dari hasil decompose:

births_dc$random %>% autoplot()

Nilai error diperoleh dari pengurangan data actual dengan data trend dan seasonal:

births_error <- births_ts - births_trend - births_seasonal

births_error %>% autoplot()

2. Menghitung secara manual decompose multiplicative model

Menggunakan data AirPassengers yang merupakan data bawaan R

head(AirPassengers)

#>      Jan Feb Mar Apr May Jun
#> 1949 112 118 132 129 121 135

class(AirPassengers)

#> [1] "ts"

Decompose time series object using decompose() function

air_dc <- decompose(x = AirPassengers, type = "multiplicative")

Cara manual decompose pada multiplicative model

Objek time series di atas merupakan objek time series dengan model multiplicative, dimana $Data=Trend\ast Seasonality\ast Error$

TREND

Mengambil nilai trend dari hasil decompose:

air_dc$trend %>% autoplot()

Lakukan smoothing pada data actual untuk memperoleh pola trend dengan metode moving average:

air_trend <- ma(AirPassengers, order = 12, centre = T)

air_trend %>% autoplot()

Seasonality

$Seasonality\ast Error=Data/Trend$

Mengambil nilai seasonal dari hasil decompose:

air_dc$seasonal %>% autoplot()

(AirPassengers/air_trend) %>% autoplot()

Berikut ini merupakan step by step untuk memperoleh nilai seasonal secara manual:

1. Nilai seasonal + nilai error diperoleh dari pembagian data actual dengan data trend

sea.err_air <- AirPassengers/air_trend

2. Mencari nilai rata-rata untuk setiap frekuensi

mean.month_air <- sea.err_air %>% 
  matrix(ncol =  12, byrow = T) %>% 
  colMeans(na.rm = T)

3. Mencari nilai rata-rata global data time series

mean.glob_air <- mean(mean.month_air)

4. Mencari nilai pembagian dari rata-rata untuk setiap frekuensi dengan rata-rata global

mean.month_air/mean.glob_air

#>  [1] 0.9102304 0.8836253 1.0073663 0.9759060 0.9813780 1.1127758 1.2265555
#>  [8] 1.2199110 1.0604919 0.9217572 0.8011781 0.8988244

5. Setelah diperoleh nilai seasonal dapat diimplementasikan untuk setiap frekuensi

air_seasonal <- ts(rep(mean.month_air/mean.glob_air, 12), start = start(AirPassengers), frequency = 12)
 
air_seasonal %>% autoplot()

Error

Error = Data / (Trend * Seasonality)

Mengambil nilai error dari hasil decompose:

air_dc$random %>% autoplot()

Nilai error diperoleh dari pembagian data actual dengan hasil kali nilai trend dan nilai seasonal:

air_error <- AirPassengers/(air_trend*air_seasonal)

air_error %>% autoplot()

Bab 9 Neural Network and Deep Learning

9.1 Neural Network and their Implementation

9.1.1 Apa perbedaan metode Machine Learning dengan Neural Network dan Deep Learning?

• Neural network bukan merupakan metode yang berasal dari statistik melainkan lahir dari pemikiran dari peneliti dengan background Computer Science dan Mathematics.
• Neural network merupakan salah satu metode Machine Learning. Neural netwrok dengan arsitektur yang cukup rumit sering disebut sebagai Deep Learning. Neural network hanya memiliki satu hidden layer, sedangkan Deep Learning memiliki lebih dari satu hidden layer.

Berikut merupakan link eksternal yang dapat dijadikan sebagai bahan referensi Deep learning & Machine learning: what’s the difference?

9.1.2 Implementasi/penggunaan deep learning di dunia nyata?

Berikut beberapa contoh implementasi/penggunaan deep learning di dunia nyata:

• Data suara:Speech emotions recognition
• Data gambar: Image recognation dengan model convolutional neural network Penggunaan deep learning saat ini:
• Top 20 Applications of Deep Learning in 2021 Across Industries

9.2 Pre-processing

9.2.1 Bagaimana cara mentransformasikan prediktor data kategorik menjadi variabel dummy?

Kita akan menggunakan data attrition yang memiliki variabel kategorik untuk dilakukan dummy transformation sebelum menggunakan metode neural network.

attrition <- read.csv("data/08-NN/attrition.csv")
str(attrition)

#> 'data.frame':	1470 obs. of  35 variables:
#>  $ attrition                 : chr  "yes" "no" "yes" "no" ...
#>  $ age                       : int  41 49 37 33 27 32 59 30 38 36 ...
#>  $ business_travel           : chr  "travel_rarely" "travel_frequently" "travel_rarely" "travel_frequently" ...
#>  $ daily_rate                : int  1102 279 1373 1392 591 1005 1324 1358 216 1299 ...
#>  $ department                : chr  "sales" "research_development" "research_development" "research_development" ...
#>  $ distance_from_home        : int  1 8 2 3 2 2 3 24 23 27 ...
#>  $ education                 : int  2 1 2 4 1 2 3 1 3 3 ...
#>  $ education_field           : chr  "life_sciences" "life_sciences" "other" "life_sciences" ...
#>  $ employee_count            : int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ employee_number           : int  1 2 4 5 7 8 10 11 12 13 ...
#>  $ environment_satisfaction  : int  2 3 4 4 1 4 3 4 4 3 ...
#>  $ gender                    : chr  "female" "male" "male" "female" ...
#>  $ hourly_rate               : int  94 61 92 56 40 79 81 67 44 94 ...
#>  $ job_involvement           : int  3 2 2 3 3 3 4 3 2 3 ...
#>  $ job_level                 : int  2 2 1 1 1 1 1 1 3 2 ...
#>  $ job_role                  : chr  "sales_executive" "research_scientist" "laboratory_technician" "research_scientist" ...
#>  $ job_satisfaction          : int  4 2 3 3 2 4 1 3 3 3 ...
#>  $ marital_status            : chr  "single" "married" "single" "married" ...
#>  $ monthly_income            : int  5993 5130 2090 2909 3468 3068 2670 2693 9526 5237 ...
#>  $ monthly_rate              : int  19479 24907 2396 23159 16632 11864 9964 13335 8787 16577 ...
#>  $ num_companies_worked      : int  8 1 6 1 9 0 4 1 0 6 ...
#>  $ over_18                   : chr  "y" "y" "y" "y" ...
#>  $ over_time                 : chr  "yes" "no" "yes" "yes" ...
#>  $ percent_salary_hike       : int  11 23 15 11 12 13 20 22 21 13 ...
#>  $ performance_rating        : int  3 4 3 3 3 3 4 4 4 3 ...
#>  $ relationship_satisfaction : int  1 4 2 3 4 3 1 2 2 2 ...
#>  $ standard_hours            : int  80 80 80 80 80 80 80 80 80 80 ...
#>  $ stock_option_level        : int  0 1 0 0 1 0 3 1 0 2 ...
#>  $ total_working_years       : int  8 10 7 8 6 8 12 1 10 17 ...
#>  $ training_times_last_year  : int  0 3 3 3 3 2 3 2 2 3 ...
#>  $ work_life_balance         : int  1 3 3 3 3 2 2 3 3 2 ...
#>  $ years_at_company          : int  6 10 0 8 2 7 1 1 9 7 ...
#>  $ years_in_current_role     : int  4 7 0 7 2 7 0 0 7 7 ...
#>  $ years_since_last_promotion: int  0 1 0 3 2 3 0 0 1 7 ...
#>  $ years_with_curr_manager   : int  5 7 0 0 2 6 0 0 8 7 ...

Kita akan melakukan cross validation, yaitu membagi data menjadi training set untuk proses pemodelan dan testing set untuk melakukan evaluasi. Namun, data train dan data test tidak langsung dimasukkan ke dalam sebuah objek melainkan dilakukan tahapan data preparation terlebih dahulu yang di dalamnya terdapat tahapan dummy transformation.

Cross validation akan dilakukan dengan menggunakan fungsi initial_split() dari library rsample. Fungsi tersebut akan melakukan proses sampling untuk cross validation dengan metode stratified random sampling, sehingga proporsi target variabel pada data awal, akan dipertahankan baik pada training set maupun testing set.

set.seed(100)

splitted <- initial_split(attrition,
                          prop = 0.8,
                          strata = "attrition")
splitted

#> <Analysis/Assess/Total>
#> <1177/293/1470>

Proses yang dilakukan pada tahapan data preparation akan dilakukan dengan menggunakan fungsi dari library recipes, yaitu:

• step_rm(): menghapus variabel yang dianggap tidak berpengaruh
• step_nzv(): membuang variabel yang variansinya mendekati 0 (tidak informatif)
• step_center() dan step_scale(): melakukan scaling
• step_dummy(): melakukan dummy transformation

rec <- recipe(attrition ~ ., data = training(splitted)) %>% 
  step_rm(employee_count, employee_number) %>%
  step_nzv(all_predictors()) %>% 
  step_center(all_numeric()) %>%
  step_scale(all_numeric()) %>%
  step_dummy(all_nominal(), -attrition, one_hot = FALSE) %>%
  prep()

Setelah mendefinisikan proses data preparation pada objek rec, selanjutnya proses tersebut diterapkan ke data train menggunakan fungsi juice() dan ke data test menggunakan fungsi bake() dari library recipes.

data_train <- juice(rec)
data_test <- bake(rec, testing(splitted))

prop.table(table(data_train$attrition))

#> 
#>        no       yes 
#> 0.8385726 0.1614274

prop.table(table(data_test$attrition))

#> 
#>        no       yes 
#> 0.8395904 0.1604096

Setelah melakukan dummy transformation pada prediktor, data train dan test harus disesuaikan bentuknya untuk melalui proses building model dengan metode neural network. Target variabel yang bertipe kategorik akan dilakukan dummy transformation dengan menggunakan fungsi to_categorical() dari library keras, sementara semua prediktor akan diubah ke dalam bentuk matriks numerik.

# menyiapkan data train
data_train_y <- to_categorical(as.numeric(data_train$attrition) - 1)

data_train_x <- data_train %>% 
  select(-attrition) %>% 
  data.matrix()

dim(data_train_x)

#> [1] 1177   44

# menyiapkan data test
data_test_y <- to_categorical(as.numeric(data_test$attrition) - 1)

data_test_x <- data_test %>% 
  select(attrition) %>% 
  data.matrix()

dim(data_train_y)

#> [1] 1177    2

9.2.2 Ketika running model Neural Network, weight/bobot diinisialisasi secara random sehingga menyebabkan hasil yang berbeda jika dilakukan berulang kali. Bagaimana cara mengatur set.seed() pada Neural Network?

Metode neural network selalu menginisialisasi bobot/weight secara random di awal, sehingga ketika metode tersebut di running berulang kali akan memperoleh hasil yang berbeda. Untuk mengatasi hal tersebut kita dapat menggunakan seed (state random). Kita dapat menentukan seed dengan menggunakan fungsi use_session_with_seed() dari library keras.

use_session_with_seed(seed)

Selain menggunakan cara di atas kita juga dapat menggunakan seed dengan fungsi initializer_random_normal(). Berikut cara menggunakan seed dengan fungsi tersebut:

# define seed
set.seed(100)
initializer <- initializer_random_normal(seed = 100)

# use the seed when building architecture
model <- keras_model_sequential() %>% 
  layer_dense(units = ..., 
              activation = "...", 
              input_shape = c(...),
              kernel_initializer = initializer, 
              bias_initializer = initializer)

9.2.3 Bagaimana cara membagi data train, test, dan validation untuk keperluan deep learning analysis?

Anda dapat menambahkan parameter validation_split saat melakukan fitting model dengan menggunakan fungsi fit() dari pacakge keras. Penjelasan lebih lengkap mengenai parameter dan fungsi dari pacakge keras dapat Anda lihat pada referensi berikut fit() function

9.3 Architecture

9.3.1 Secara best practice, berapa jumlah hidden layer dan nodes yang digunakan dalam membangun arsitektur neural network (ANN)?

• Kebanyakan peneliti menggunakan minimal 2 hidden layer, namun tidak menutup kemungkinan menggunakan lebih dari 2 ataupun kurang dari 2 hidden layer.
• Jumlah nodes biasanya semakin sedikit ketika hidden layers semakin dekat dengan output layer. Tujuannya adalah untuk melihat fitur dengan lebih spesifik.
• Kebanyakan peneliti menggunakan angka biner $2^n$ seperti 1, 2, 4, 8, 16, 32, 64, 128, 256, dst karena neural network merupakan metode yang berasal dari bidang IT dan Matematika yang biasa menggunakan angka biner.

9.3.2 Fungsi aktivasi apa yang sering digunakan ketika membuat arsitektur neural network?

• Hidden layer: relu (Rectified Linear Unit), karena dapat mentransformasi data dengan mengubah nilai negatif menjadi 0 dan membiarkan nilai positif. Hal ini mengakibatkan semakin mendekati output layer, informasi yang dibawa tidak banyak berkurang.
• Output layer: tergantung case yang sedang dikerjakan:
  • Regresi: linear
  • Klasifikasi biner: sigmoid
  • Klasifikasi multiclass: softmax

9.3.3 Bagaimana cara menentukan batch size dan jumlah epoch?

• Batch size menggunakan angka yang dapat habis membagi jumlah data, agar data yang tersedia dapat digunakan secara keseluruhan (tidak ada yang tidak terpakai). Contoh: Jika data train terdiri dari 800 observasi, kita bisa menggunakan batch size 200 yang dapat habis membagi 800 observasi tersebut menjadi 4 batch.
• Jumlah epoch dimulai dari angka yang kecil terlebih dahulu untuk memastikan bahwa model dapat berjalan tanpa error sehingga tidak menunggu komputasi yang terlalu lama. Kemudian lihat apakah error dan accuracy yang dihasilkan sudah konvergen atau belum. Apabila belum, silahkan tambahkan jumlah epoch sedikit demi sedikit, dan sebaliknya.

9.3.4 Bagaimana menentukan learning rate yang tepat?

Learning rate dapat mempercepat atau memperlambat besaran update error.

• Semakin besar learning rate, maka error/accuracy akan semakin cepat konvergen. Namun, bisa saja titik error paling minimum (global optimum) terlewat.
• Semakin kecil learning rate, maka terdapat kemungkinan yang lebih besar untuk sampai di titik error paling minimum (global optimum). Namun, error/accuracy akan membutuhkan waktu lebih lama untuk konvergen.

9.3.5 Optimizer apa yang paling sering digunakan?

Optimizer merupakan fungsi yang digunakan untuk mengoptimumkan error (memperkecil error). Secara sederhana, untuk mengoptimumkan suatu fungsi bisa melalui fungsi turunan, pada neural network disebut sgd (Stochastic Gradient Descent). Namun, sgd memiliki beberapa kekurangan sehingga mulai banyak peneliti yang memperbaiki fungsi sgd tersebut.

Salah satu optimizer yang cukup terkenal adalah adam sebagai optimizer yang merupakan perbaikan dari sgd karena optimizer tersebut dapat mengupdate/menyesuaikan momentum ketika proses optimisasi. Berikut link eksternal yang dapat dijadikan sebagai bahan referensi Adaptive Moment Estimation (Adam)

Selain tips di atas berikut link eksternal yang dapat dijadikan referensi dalam membangun arsitektur neural network Rules-of-thumb for building a Neural Network

9.3.6 Adakah fungsi untuk memvisualisasikan arsitektur neural network?

Anda dapat menggunakan fungsi plot() untuk memvisualisasikan arsitektur model neural network yang dibuat dengan fungsi neuralnet() dari pacakage nnet seperti berikut

set.seed(100)
nneu <- neuralnet(y ~ Var1 + Var2 + Var3, dat, hidden = 4, rep = 5)
plot(nneu, rep = "best")

9.4 Framework

9.5 Mathematics Formula

Aturan update weight:

1. Menghitung turunan parsial dari weight.

2. Berikut hal yang harus dilakukan jika:

   • Hasil turunannya Positif, maka nilai weight dikurangi.
   • Hasil turunannya negatif, maka nilai weight ditambah.

   Keduanya dilakukan dengan tujuan untuk mencari weight yang menghasilkan error terkecil.

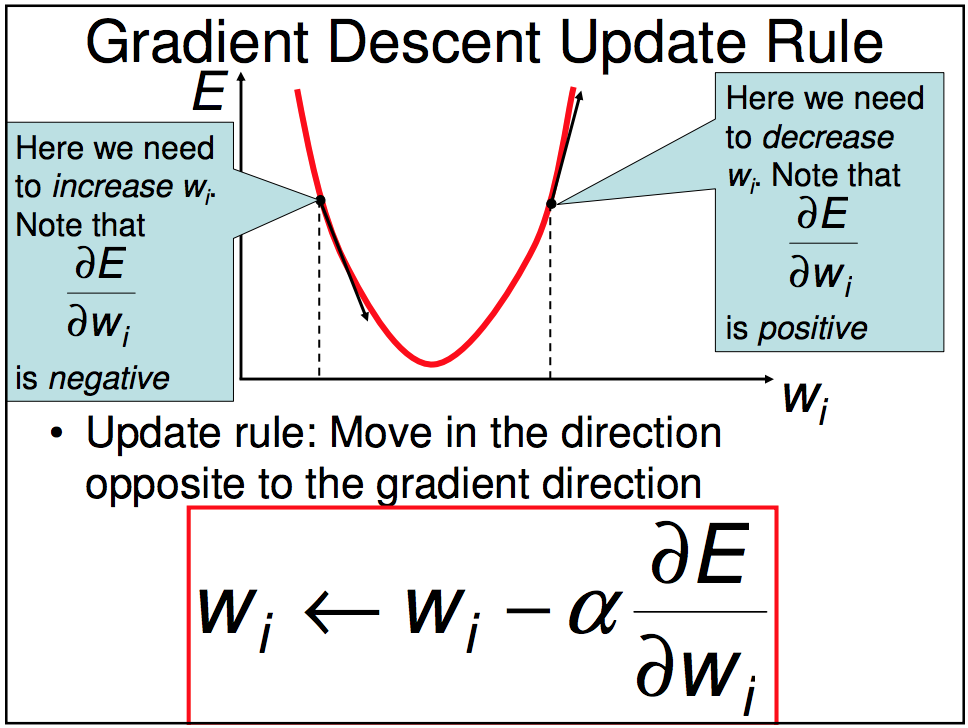
Forward Propagation

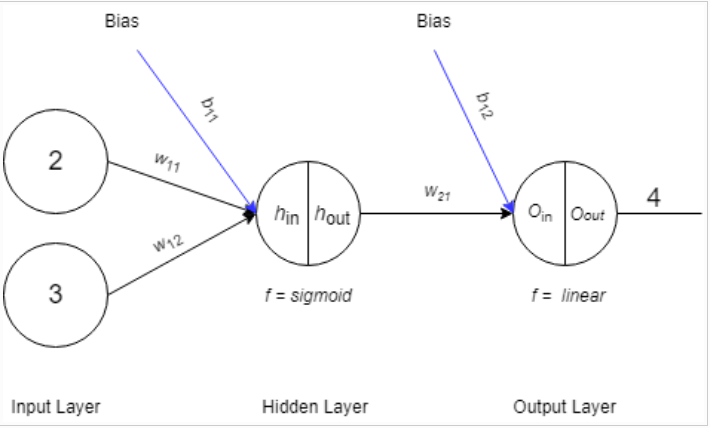
Diketahui:

• $w_{11}=0.5$
• $w_{12}=1$
• $b_{11}=1$
• $w_{21}=0.5$
• $b_{12}=1$

1. Forward pass dari input ke hidden layer 1.

$$h_{in}=x_1\ast w_{11}+x_2\ast w_{12}+b_{11}{h}_{in}=2\ast 0.5+3\ast 1+1h_{in}=5$$

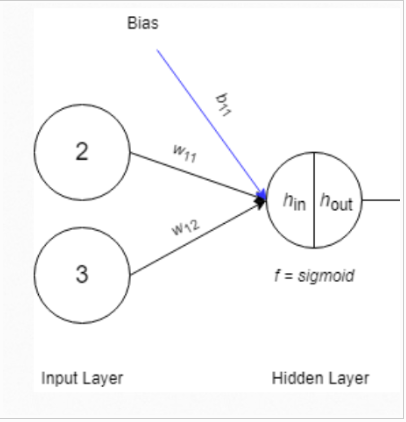
2. Transformasi nilai dengan fungsi aktivasi sigmoid.

$$sigmoid=\frac{1}{1+e^{-x}}$$

$$h_{out}=\frac{1}{1+e^{-5}}{h}_{out}=0.9933071$$

3. Forward pass hidden layer ke output layer.

$$Outpu{t}_{in}=0.9933071\ast 0.5+1Outpu{t}_{in}=1.496654$$

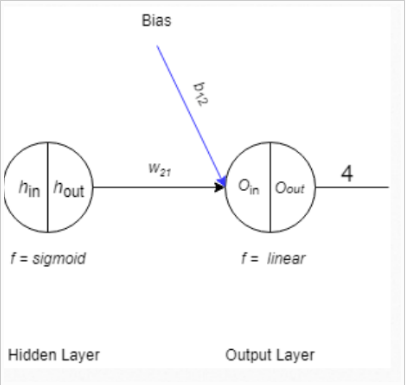
4. Transformasi nilai dengan fungsi aktivasi linear.

$$Outpu{t}_{in}=Outpu{t}_{out}=1.496654$$

5. Hitung nilai error dengan cost function.

$$cost=\frac{1}{2}(outpu{t}_{aktual}-outpu{t}_{out}{)}^{2}cost=\frac{1}{2}(4-1.496654{)}^{2}cost=3.133371$$

Backpropagation

1. Backward pass dari output ke hidden layer 1

2. Mengitung turunan parsial cost ke $w_{21}$ menggunakan chain rule:

$$\frac{d_{cost}}{d_{w_{21}}}=\frac{d_{cost}}{d_{outpu{t}_{out}}}\ast \frac{d_{outpu{t}_{out}}}{d_{outpu{t}_{in}}}\ast \frac{d_{outpu{t}_{in}}}{d_{w_{21}}}$$

Hitung $\frac{d_{cost}}{d_{outpu{t}_{out}}}$

$$\frac{d_{cost}}{d_{outpu{t}_{out}}}=\frac{d\left(\frac{1}{2}\right(outpu{t}_{actual}-outpu{t}_{out}{)}^2)}{d\left(outpu{t}_{out}\right)}\frac{d_{cost}}{d_{outpu{t}_{out}}}=-1\ast 2\ast \frac{1}{2}(4-1.496654)\frac{d_{cost}}{d_{outpu{t}_{out}}}=-2.503346$$

Hitung $\frac{d_{outpu{t}_{out}}}{d_{outpu{t}_{in}}}$

karena merupakan fungsi aktivasi linear maka:

$$\frac{d_{outpu{t}_{out}}}{d_{outpu{t}_{in}}}=1$$

Hitung $\frac{d_{outpu{t}_{in}}}{d_{w_{21}}}$

$$\frac{d_{outpu{t}_{in}}}{d_{w_{21}}}=\frac{d(h_{out}\ast w_{21}+b_{12})}{d\left(w_{21}\right)}\frac{d_{outpu{t}_{in}}}{d_{w_{21}}}=h_{out}\frac{d_{outpu{t}_{in}}}{d_{w_{21}}}=0.9933071$$

Jadi turunan parsial $\frac{d_{cost}}{d_{outpu{t}_{out}}}$:

$$\frac{d_{cost}}{d_{outpu{t}_{out}}}=-2.503346\ast 1\ast 0.9933071\frac{d_{cost}}{d_{outpu{t}_{out}}}=-2.486591$$

3. Mengitung turunan parsial cost ke $b_{12}$ menggunakan chain rule:

$$\frac{d_{cost}}{d_{b_{12}}}=\frac{d_{cost}}{d_{outpu{t}_{out}}}\ast \frac{d_{outpu{t}_{out}}}{d_{outpu{t}_{in}}}\ast \frac{d_{outpu{t}_{in}}}{d_{b_{12}}}\frac{d_{cost}}{d_{b_{12}}}=-2.503346\ast 1\ast 1\frac{d_{cost}}{d_{b_{12}}}=-2.503346$$

4. Update $w_{21}$

Misal, learning rate ($\alpha$) = 0.1,

$$w_{21}^{{}^{\prime }}=w_{21}-\alpha \left(\frac{d_{cost}}{d_{w_{21}}}\right)w_{21}^{{}^{\prime }}=0.5-(0.1\ast -2.486591)w_{21}^{{}^{\prime }}=0.7486591$$

5. Update $b_{12}$

$$b_{12}^{{}^{\prime }}=b_{12}-\alpha \left(\frac{d_{cost}}{d_{b_{12}}}\right)b_{12}^{{}^{\prime }}=1-(0.1\ast -2.503346)w_{21}^{{}^{\prime }}=1.250335$$